Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Odesolve
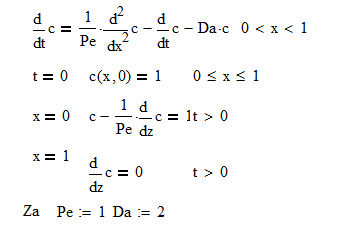
Hello eveyone..
Can someone please help me of solving this problem by using Odesolve.
I have to solve numerically the dimensionless mathematical model of unsteady pipe reactor where the reaction takes place the first order.
Best regards, Milica
P.S. Sorry for bad English
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have a PDE not an ODE so you need to use pdesolve. Pdesolve doesn't exist yet in Prime so you will have to use Mathcad 15 or earlier. Numol should also work if you change the boundary conditions as I discuss below.
I'm not sure, but I think pdesolve won't be able to handle the Dankwert's boundary conditions. You probably will need to set the inlet concentration = 1 and dc/dx=0 at x=0. The exit derivative = 0 is not realistic for all reactors. It is also not realistic to believe that a reactor would somehow know how to perform upstream in order to satisfy the exit condition. Thus, the boundary conditions need to be set at the inlet.
You also have an error in the first line: you have dcdt twice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for your reply. You are right, it is PDE. I am trying to solve problem with Pdesolve but MathCad displays an error. Can someone please help me?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The argument in the Pdesolve list should only be c, not c(x,y) or c(x,t). Also, your PDE still has too many dc/dt terms.
I have discovered that Pdesolve does allow the mixed boundary condition. In fact, that is the only boundary condition that you need. The exit boundary condition you have will lead to a non-realistic result. It will force the reaction to complete regardless of the reactor length. Try it.
Update: The c variable being assigned to the pdesolve result should also not have arguments.
c:= pdesolve(c,x,....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was wrong about Numol: it will not handle these boundary conditions. Numol requires that the boundary conditions be specified at both boundaries (which your problem meets) but it also requires that both conditions be of the same type, Diriclhet or Neumann. Neither of those choices fit your case.
I noticed that the Pe=1 you are using is a typical value for fixed beds but the characteristic length is one particle diameter. Such a Peclet number might be valid for a gauze bed reactor, but not for typical reactors. For a typical fixed bed reactor, the Peclet number needs to be multiplied by L/dp, reactor length/particle diameter.
Eventually, you will probably find that axial dispersion is not important for typical fixed be or open tube reactors. It only becomes a factor for the unique, very short reactors, like the platinum gauze reactors. Thus, that axial dispersion term can be eliminated from a model and the problem with the exit boundary condition is avoided.





