Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One optimization problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One optimization problem
Do you know one symbolic solution of this problem?
See please one numerical solution in attach (M15):
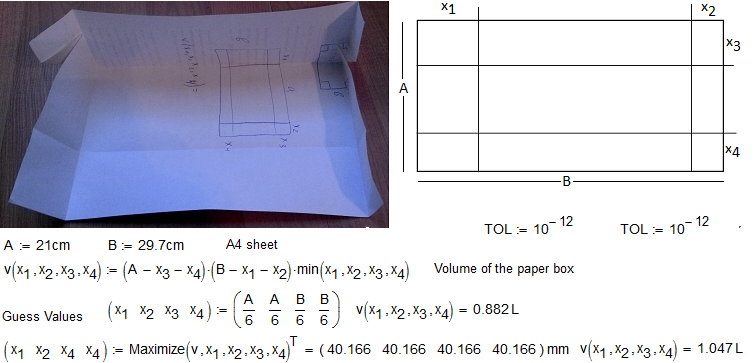
PS At A=B x=A/6
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Nice, I like it. I am no specialist but the algorithm demonstrated here seems to be neither Conjugate Gradients nor Quasi Newton.
It would be better and informative to trace and graph the behaviour of Mathcad's built-in algorithms - maximize() in our case here.
My simple algorithm (see above) is in this problem the best!
See please:
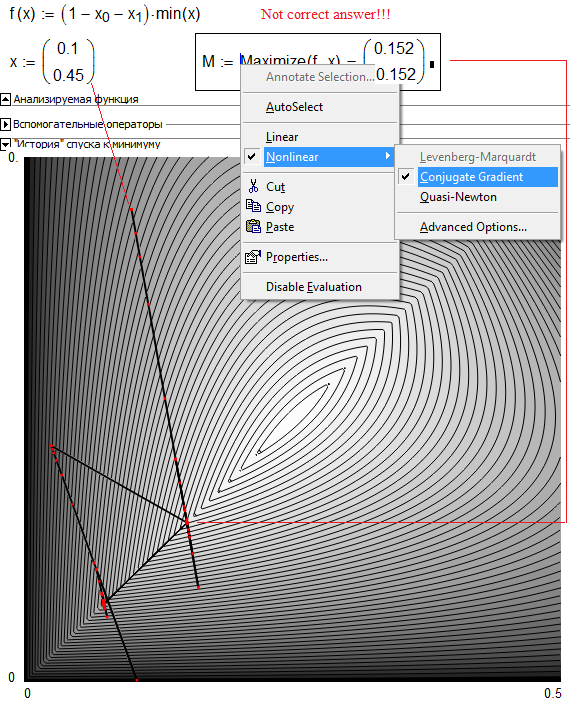
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
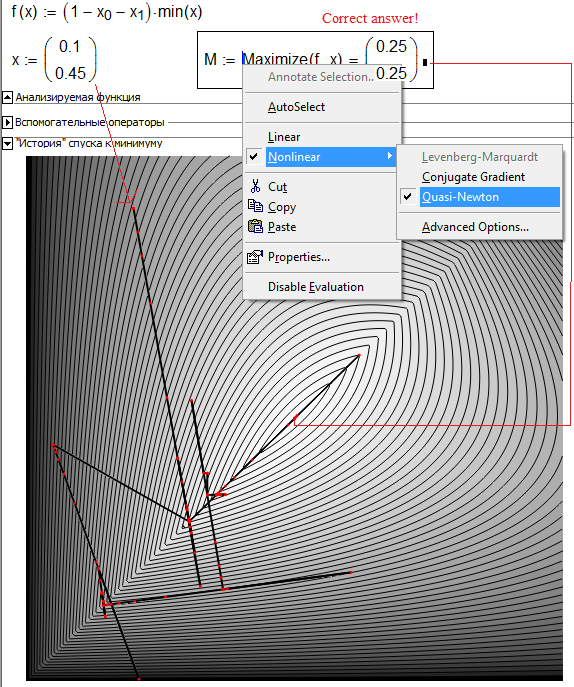
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, indeed. Sometimes in special cases the more general and usually robust algorithm may fail and a simpler one would do the job.
Especially as the maximum in this tasks is not where the gradients are zero and no unique derivative exists in the area of the max, algorithms that rely on derivatives tend to fail.
More than 200 steps and CG is still far away:
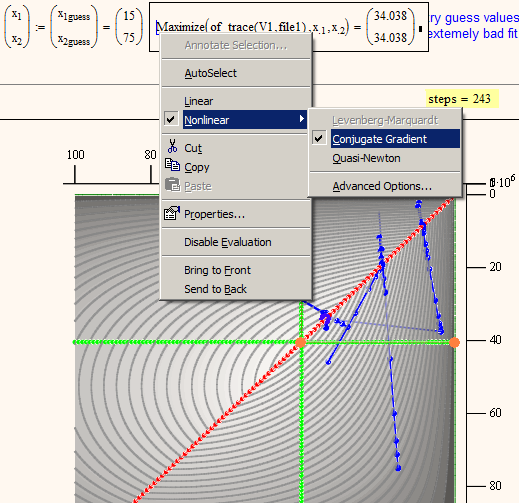
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also funny to look at the algorithm in 3D. Again a pic from CG here.
I don't know how the algorithm is implememented in Mathcad but its noticable that it will make rather big steps at some points an then it will from time to time try the same pair of guess values two or more times in a row - that doesn't make sense to me!? See the attached data file which shows the (x1,x2) values the algorithm will try its luck with.
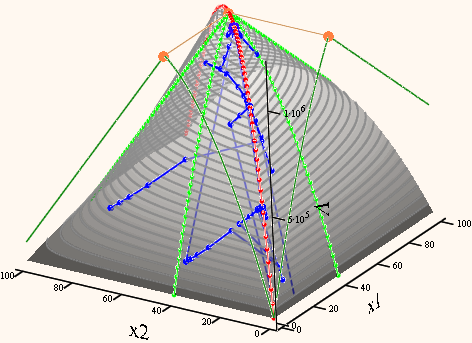
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Also funny to look
I hope it is funny too http://twt.mpei.ac.ru/ochkov/Coriolis/Coriolis_Eng.htm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, but I'd rather stay within the subject of the thread otherwise things are going to confusing for me 😉
In fact its easier to trace self written algorithms than the encapsuled ones built into Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This "quadrate" problem in a N-field - see the picture.
Do you have any solution for a "non quadrate" problem with the function v(x, A, B, n)?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you think in n dimensions and want to go from the hypercube to a hypercuboid (? I am absolutely not sure about the wording here), we would not only have A and B but rather A1 ... An !
And as the discussion has shown here, we can not be sure that the solution would be a local maximum of the objective function.
Good luck! ![]()
BTW, you could try to constrain x<A/2 with assume to get rid of the unwanted "solutions".
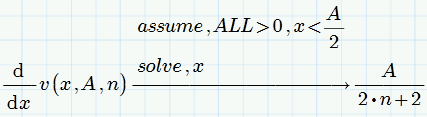
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As we just traced the built-in maximize() algorithm - a question for those who know:
Whats the best way way to trace an internal algorithm? I can think of three ways and have sucessfully implemented two of them (and am not that happy with). That is using Mathcad's trace and then copy and paste 😞 or let Mathcad write the data to a file in every single iteration step (which I did in the file above).
Third idea (and maybe best way?) would be the use of a scripted component which collects the data during iteration - not sure about the implementation, though.
Any other ideas?
PS: @Valery: How was it done in the file you posted the screenshot of?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
PS: @Valery: How was it done in the file you posted the screenshot of?
Copy and paste
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PS: @Valery: How was it done in the file you posted the screenshot of?
Copy and paste
So that I am clear - you had second objective function f(x) in the collapsed area which had a trace-command or used a solve block with a dummy function inside there and then copied the data from the debug window?
- « Previous
-
- 1
- 2
- Next »





