Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Parametric Optimization With Constraints as Parameters?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Parametric Optimization With Constraints as Parameters?
I have been trying to set up a constrained minimization problem parametrically, so it behaves rather like a function. From reading previous discussions, I understand that solve blocks cannot be placed in programs. However, the Quicksheet on Constrained Nonlinear Optimization shows that it's possible to parameterize some parts of an optimization, specifically, (1) the guess values, and (2) additional parameters of the objective function that are not involved in the optimization. I've attached the Quicksheet with those two items highlighted.
BUT... is it possible to parameterize the constraints? For example, the values 2 and 9 in the Quicksheet's constraints. Ideally, one would write a program containing the solve block, but that's not supported. Any workaround?
Thanks in advance to any of you who can shed light on this. And thanks to Valery Ochkov for explaining where to post questions or discussions.
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BUT... is it possible to parameterize the constraints? For example, the values 2 and 9
Sure! Simply replace those values by variables (lo,hi) and add those variables as arguments to the function you create AND (and thats the trick) also as arguments to the objective function even though they are not used there anyway - the order of the arguments does matter, so take care or you may get wrongs results!.
You may even use completely different constraints by turning the constraint into a function and use the function name as argument. It all depends on your needs.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May be it helps you:
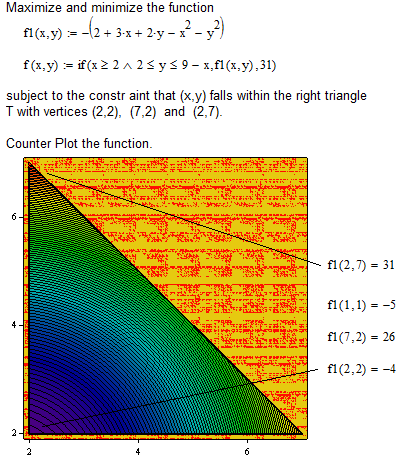
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This should work - thank you. One would have to know in advance the approximate value of the minimum (or maximum) in order to assign values that make regions outside the constraints uninteresting to the solver, I think. But often we do know in advance at least order of magnitude estimates of min (or max).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BUT... is it possible to parameterize the constraints? For example, the values 2 and 9
Sure! Simply replace those values by variables (lo,hi) and add those variables as arguments to the function you create AND (and thats the trick) also as arguments to the objective function even though they are not used there anyway - the order of the arguments does matter, so take care or you may get wrongs results!.
You may even use completely different constraints by turning the constraint into a function and use the function name as argument. It all depends on your needs.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Brilliant! It works. Using the constraint parameters as dummy arguments of the objective function would never have occurred to me. Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using the constraint parameters as dummy arguments of the objective function would never have occurred to me.
I also ever so often forget about it. In a recent thread I even claimed that maximize can't be turned into a function because I tried to do and forgot about those dummy arguments.
But Mathcad's help about Minimize/Maximize is mentioning it (while they don't stress the importance of the order of arguments):
"Output may be assigned to a single variable, a vector of explicit variable names, or a function of argument names in the objective function. The resulting parameterized solve block can be used either to supply guess values for the solved variables in the objective function, or to supply parameters in the objective function or the constraints after the block. Even if the parameters don't appear in the objective function, they must be named as an argument to the function."





