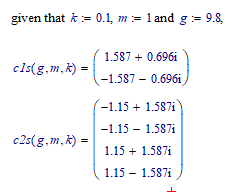- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
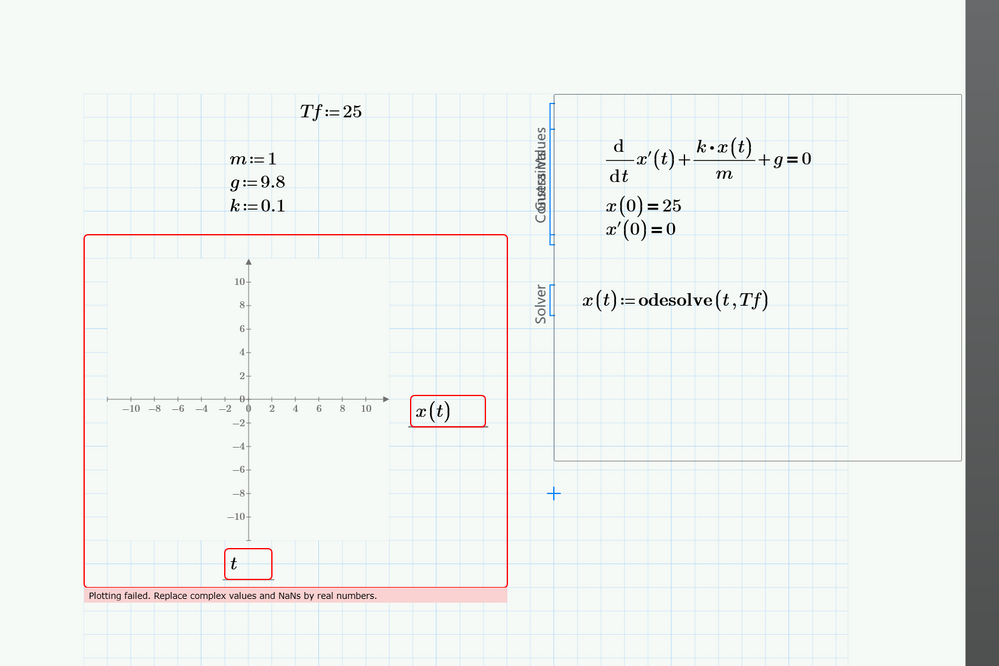
Plotting failed. Replace complex values and NaNs by real numbers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Plotting failed. Replace complex values and NaNs by real numbers.
Hi, I'm fairly new to Mathcad. Trying to plot the solution to a differential equation but I can't seem to get it working. I've attached the necessary files.
Thanks!
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
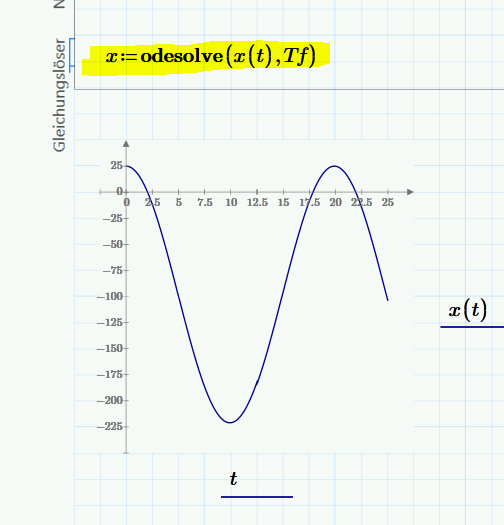
You used a wrong syntax for odesolve!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
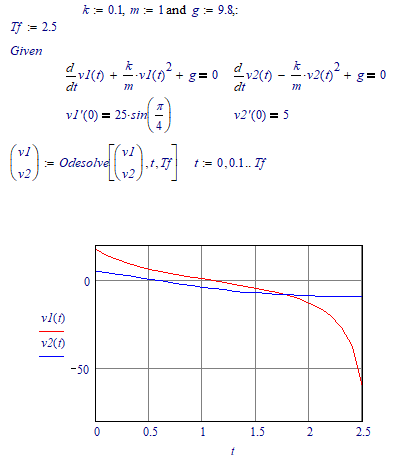
Sorry to bother you again, whenever I raise x(t) to the 2nd power, so: x(t)^2 the odesolver breaks. It gives me: Unkown error.
Any idea how to fix this?
heres the code, I changed x to v.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As v1 and v2 are independent from each other I would rather use a separate solve block for each of them.
But it should work the way you has done, too.
The problem is the equation for v1. when t increases, v1(t) decreases dramatically and Primes algorithm would fails because it does not converge,
You may look for the equation if its correct.
Only solution so far seems to be to set Tf to a lower value. Tf=2.65 seems to be the largest value possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Thanks for the response, it works perfectly now. Thank you so much!
The equation is fine, its just that the equation has a 'limit' before it becomes 'invalid'.
These are the equations of motions with air resistance, the projectile goes up, both gravity and friction work against it but once it reaches the top and goes down, only friction works against the ball, which is where the second equation comes in.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
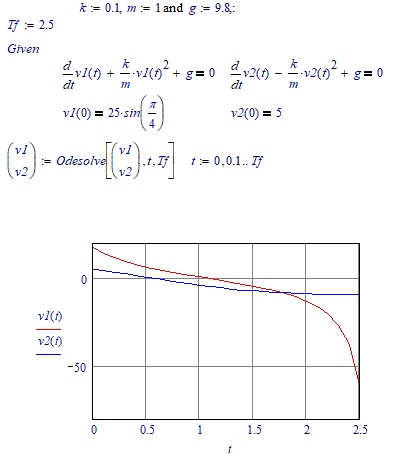
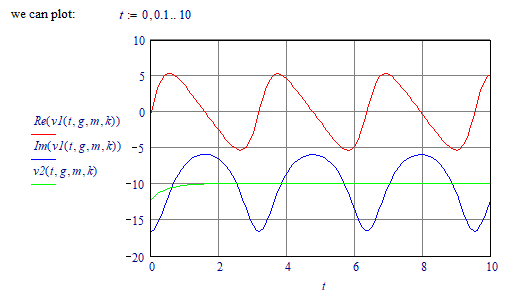
This can't be right, or am I looking wrong...
The derivative of v2 w.r.t. time t must be 5 at t=0. I see the black trace (for v2) in the graph go down when t is going up from 0.
Likewise for v1. The derivative of v1 must be 25sin(pi/4) {about 17} at t=0. I see the red trace going down there.
I get the same results in Mathcad 11: When the initial conditions are specified with primes ('):
As well as when they are given without:
Turning to the help info, it says that the initial conditions MUST be given for the primitive function(s) and its/their derivative(s) up to an order one less than the order of the DE, at a single point.
Mathcad (and apparently Prime as well) simply ignore the prime...? How does Mathcad 15?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
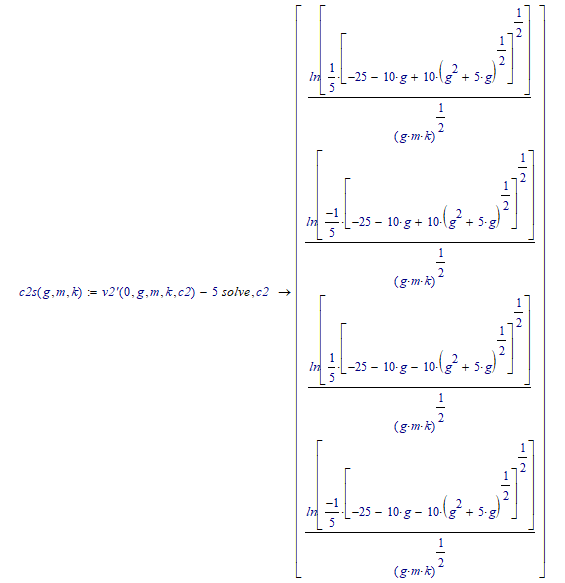
But before I found that I had it solved symbolically:
Notice that:
The above is based upon the set of differential equations given.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
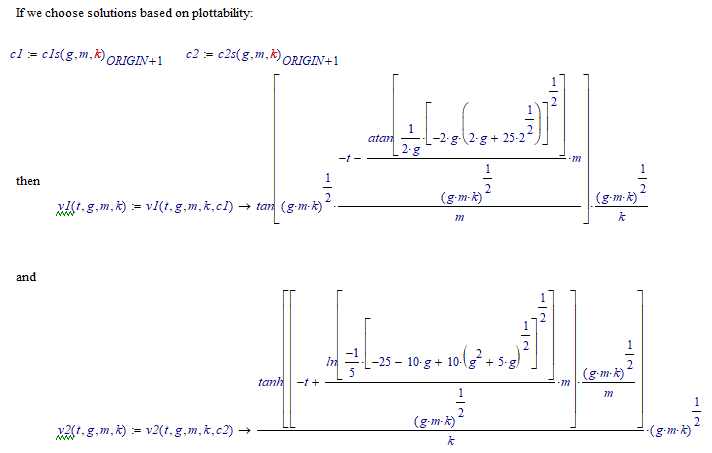
BUT, if the initial conditions were meant to be v1(0)=25*sin(pi/4) and v2(0)=5, then the Odesolve solution is OK, and the symbolic solution is:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc!
Thanks for your response and excellent explanation.
I was going over it and indeed I messed up some things. Thanks for pointing it out!