Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Plotting failed. Replace complex values and NaNs by real numbers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Plotting failed. Replace complex values and NaNs by real numbers.
Hello,
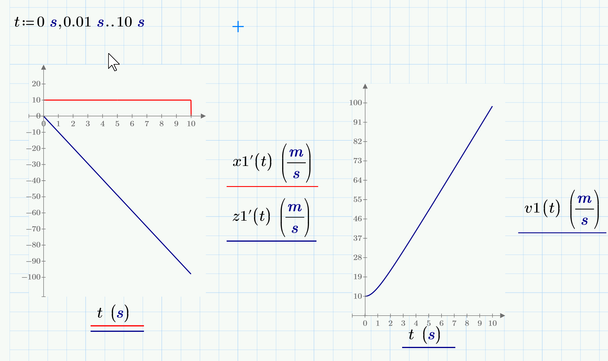
I am new to MathCad. I plotted the freefall equation and solved for x and z. Then I would like to plot the velocity, so x' and z' but get the error: "replace with complex values and NaNs by real numbers". It shouldn't have complex values and NaNs, I have checked the odesolve syntax, the time step and the units, but still can't find the mistake.
Would appreciate help! The file is attached.
Thanks in advance!
Ln
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may consider using a simple range variable for t rather than the vector you used.
I am not quite sure why Prime has problems with the way you had set up the sheet - it should work OK. But Prime seems to have problems with the combination of the vector t and the derivative operator. We may call it a bug.
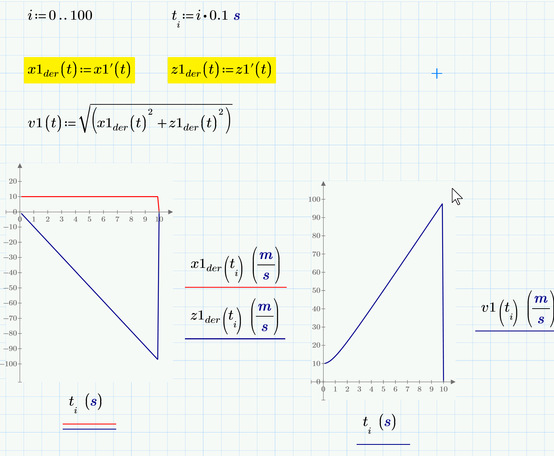
Another way around this problem/bug is to define the derivatives as separate functions and use these:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's something weird going on in your sheet.
The two functions x1'(t) and z1'(t) are not defined which I think is what causes the error message for your plot.
But I would have expected an error message at the definition of v1(t), which uses those two undefined functions.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hey Luc,
I thought it is enough to define the u0 and v0, and when solving x and z, it should calculate x'(t) and z'(t). If I insert a single value for t, I also get a plausible answer.
Do you have an idea why I get these results as well as the plot v1(t)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> The two functions x1'(t) and z1'(t) are not defined
No, its the derivative operator which should be fully functional in Prime (in real Mathcad we could only use it in a solve block with odesolve).
As written in my answer to the OP I consider it a bug of Prime as it looks like its the combination of vector argument and derivative operator which causes that error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may consider using a simple range variable for t rather than the vector you used.
I am not quite sure why Prime has problems with the way you had set up the sheet - it should work OK. But Prime seems to have problems with the combination of the vector t and the derivative operator. We may call it a bug.
Another way around this problem/bug is to define the derivatives as separate functions and use these:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok, thank you Werner!