Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Prime 3.1 Column vs Row operator performance difference?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 3.1 Column vs Row operator performance difference?
In the thread Re: Similar to vector matrix product, but different… the poster put the return value from a program inside the loop, which you don't normally see.
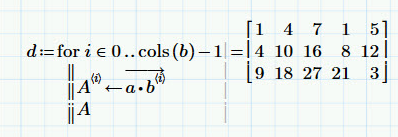
Out of idle curiosity, I wondered if it had any effect on Mathcad's performance by doing this rather than placing the return value outside of the loop. I also wondered what effect using the Prime row operator would make and doing without the vectorized multiplication. What I found rather surprised me, in that the row operator method was considerably faster than the original column method. I looked at doing array expansion by replicating a column-wise to conform with b and then doing Hademard (element-by-element) multiplication. I also tried transposing b, multiplying each "column" by its corresponding vector element and then transposing the result. This is what I found (on an i7 with 8 GiB RAM running Windows 10).

I was surprised to see that the row operator method was so quick. I wonder if the internal order of array storage is row-wise rather than column-wise (which I'd kind of expect given that Mathcad deals with column vectors)? I also did the same test (minus the row operator) in Mathcad M15 M040 and got the following result ... considerably slower in all cases and not much to choose between them.

Stuart
- Labels:
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
In the thread Re: Similar to vector matrix product, but different… the poster put the return value from a program inside the loop, which you don't normally see.
Out of idle curiosity, I wondered if it had any effect on Mathcad's performance by doing this rather than placing the return value outside of the loop. I also wondered what effect using the Prime row operator would make and doing without the vectorized multiplication. What I found rather surprised me, in that the row operator method was considerably faster than the original column method. I looked at doing array expansion by replicating a column-wise to conform with b and then doing Hademard (element-by-element) multiplication. I also tried transposing b, multiplying each "column" by its corresponding vector element and then transposing the result. This is what I found (on an i7 with 8 GiB RAM running Windows 10).
I was surprised to see that the row operator method was so quick. I wonder if the internal order of array storage is row-wise rather than column-wise (which I'd kind of expect given that Mathcad deals with column vectors)? I also did the same test (minus the row operator) in Mathcad M15 M040 and got the following result ... considerably slower in all cases and not much to choose between them.
Mystery solved and its' not really a mystery. The array storage does indeed appear to be columnwise. However, it takes time to extend an existing array and this is what's happening as the for loops iterate through the columns. At each iteration, a new column is added to A and Mathcad spends time doing this.
However, when operating on rows, Mathcad Prime appears to be more efficient at creating the necessary memory (even though (for a square array) the same number of elements are added). I don't know why this should be.
A standard Mathcad method of improving execution time when creating large arrays is to predefine the array; this means that Mathcad merely has to replace elements of the array rather than extend it, and this is a quicker operation. The easy way to check this is to reverse the order of iterating across the columns. As can be seen, this results in a significant reduction in execution time for the column operations.
Mathcad 15: (r = reverse column indexing version)

Prime 3.1

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I confirm. For a large array you can have good performances by allocating first the storage an then processing.
You can do that in programming block. You just need to set a value for the last member of the vector (or matrix) (usually I set this to zero).
This is true for Mathcad 14 (and 15 I guess).
Now I'm finally moving to Prime! It took years to have a version working with Italian keyboards (not supported properly up to 3.1). But now it seems to work and I've just downloaded the trial. 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Slow speed





