Hi,
I would really appreciate if you can help me on this symbolics equation!! Thanks in advance !!
There is a problem when I use the keyword "Find" to solve the following symbolics equation .
It actually pretty simple equation: I have 6 unknown variables in 6 equation, and I want to get all the unknown parameters in symbolics expression with other known parameters.
As already written here http://communities.ptc.com/docs/DOC-5312#comment-13319
I can reduce the first five equations to a simple equation which conflicts with the last one, as we get
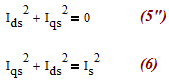
See the attached file for the derivation of it.
In the file of my previous post in the text after (5') please delete the word "only" and change the "to" to "two". 😉
Here is a more formalistic and compact approach, but the result is the same:
We can try to solve EQ5b alone for the two variables and if we use "fully" we get
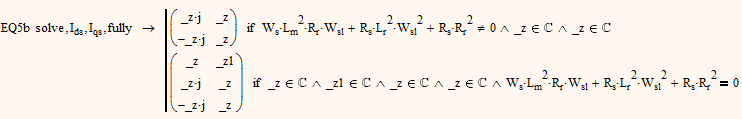
which means that if the second bracket term is not zero, we can chose any number for one of the variables and the other will be this number multiplied by +j or -j (only real solution is 0,0.
If the second bracket term is zero, Mathcad adds a third pair of solutions at the top of its solution vector which says we can chose any number for any variable - its unnecessary that Mathcad still keeps the other two lines.
If we try to solve EQ5b AND EQ6 we normally would get that "no solution found" but if yw use "fully" we get
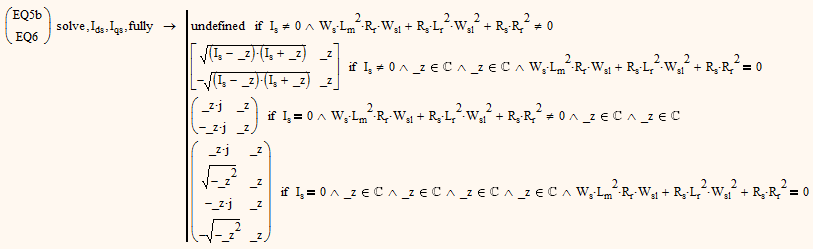
The first line is the general case (neither the bracket term nor I.s are zero and so there is no solution. The other lines are the special cases, neither of them has a unique solution, though.
We get a slightly more compact view if we use "simplify"
