Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem with the solver Odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem with the solver Odesolve
Hi!
I'm trying to solve the deflection of a beam with a constant load along it's length.
I have a differential equation of 4th degree with four initial conditions.
The moments in the bearings are zero and the deflections too.
Now my question is: Why don't i get a solution with "Odesolve" in MP4 although i initialized all four conditions completely?
Without Units, it works!
The Error Message is:

Any help will be appreciated
Thank you.
Best Regards, Volker
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" I need a quick solution like creating a short solve block working with units."
Attached is your quick solution with units. Note that you can make both I and q functions of position along the beam.
Enjoy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Volker,
In my opinion, being the differential equation of the fourth order, the initial conditions for the first and third derivatives of y are missing.
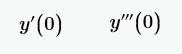
In fact, by solving analytically with Laplace, the given equation, I need all the initial conditions, as can be seen from the following calculation:
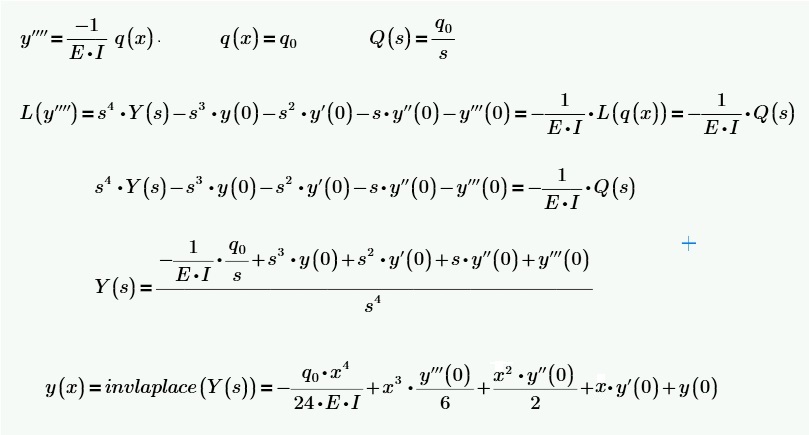
Greetings
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> In my opinion, being the differential equation of the fourth order, the initial conditions for the first and third derivatives of y are missing.
They aren't missing - you simply solve a different problem.
In Volkers problem we know the values of y and y'' at the end of the interval instead (something Mathcads odesolve ever so often has its problems with).
Volker already told us and Fred had shown that the information is sufficient and odesolve is able to solve if no units are used.
So it looks like Prime cannot deal with units that perfect as we may have thought and wished.
At least I could not spot any error in the way Volker had set up the problem and the "unknown exception error" thrown may indicate a bug in Prime.
Maybe someone finds it worth the trouble to report the bug.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It could be said that mathcad automatically considers null the initial conditions missing in the solution block, which are, instead, present in the analytical solution. So there is a certain probability of error in the mathcad solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> It could be said that mathcad automatically considers null the initial conditions missing in the solution block,
No, it doesn't. Mathcad does not assume any specific start value. It determines the start value of the independent variable from the inititial conditions you have to provide.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will send the File with the error message and the link from my thread to PTC- let's see what they say to this.
...to be honest, I do not believe that in MP5 the problem will be solved beside many others.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No initial conditions are missing, you just have to treat them right. The ODE is defined with:

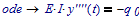
Then the solution is (in terms of the above):
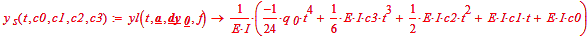
Now we have to find c0 through c3 knowing ys(0)=ys''(0)=ys(l0)=ys''(l0)=0:

That gives:
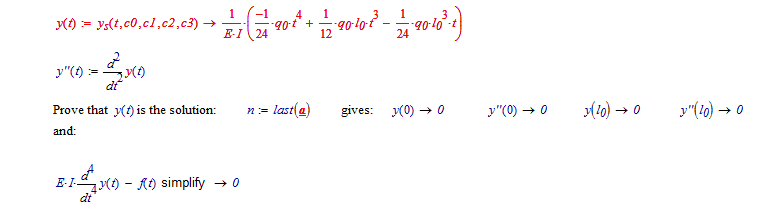
Proves thta the DE is solved, and the initial conditions are met.
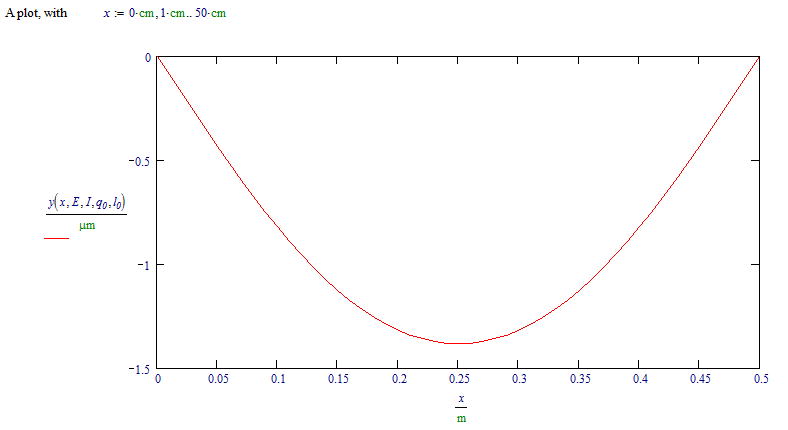
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Impressive!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If it works without units, then do it without units. (Like we did in version 15!)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
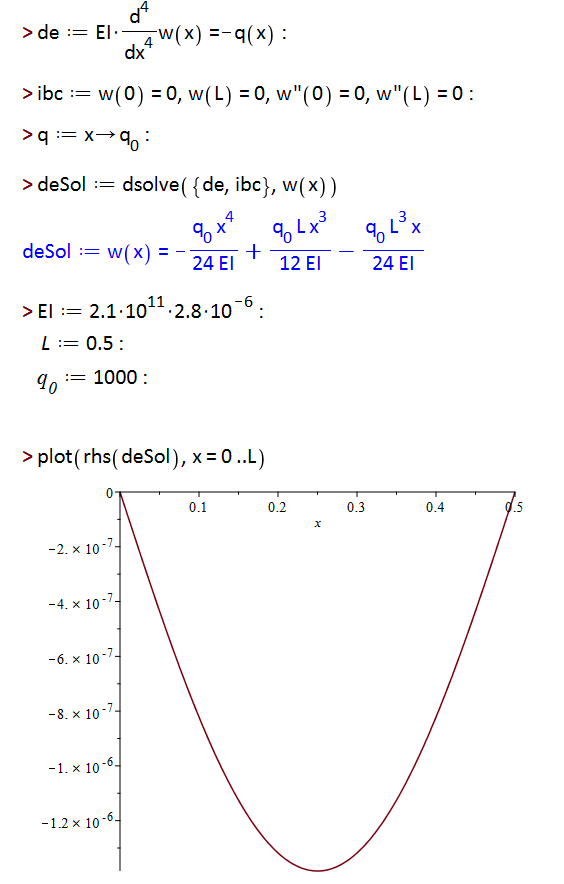
Symbolic solution from Maple. If you want more complicated loading conditions (like partially distributed load plus several point loads) then Maple will give the symbolic deflection/moment/shear equations (it won't handle units in the ODE, though).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to all, but i need a quick solution like creating a short solve block working with units.
I want a quick numerical solution- a short solution like engineers want to have for work.
When having a beam for example with 4 forces and a moment, the symbolical solution kills time and is not practical.
Best regards, Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" I need a quick solution like creating a short solve block working with units."
Attached is your quick solution with units. Note that you can make both I and q functions of position along the beam.
Enjoy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Fred!
That hit the nails head.
I have now a short numerical solution with units at the end.
The function "UnitsOf" was new to me.
Thanks to all for your efforts.
Best regards, Volker





