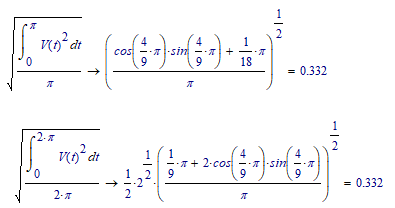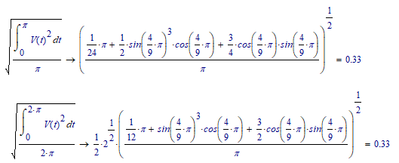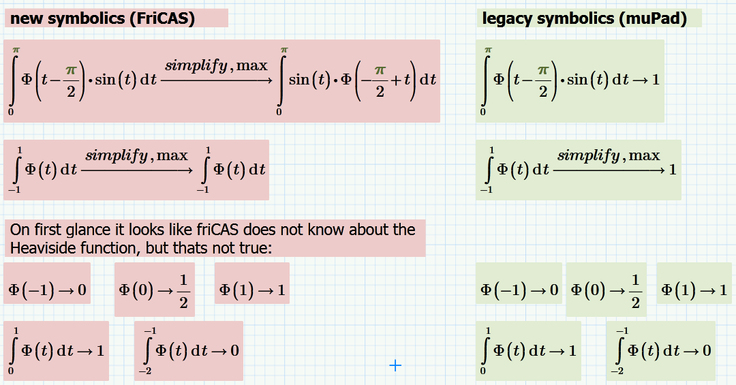Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
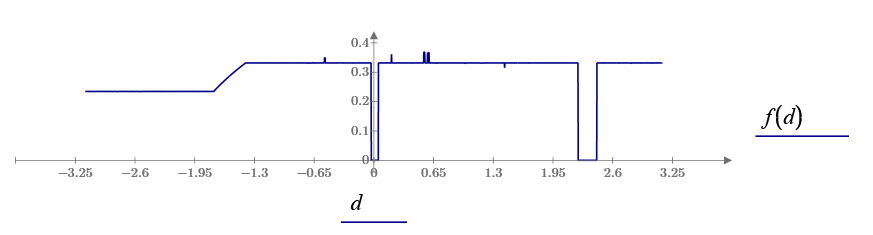
RMS bug.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about this approach?
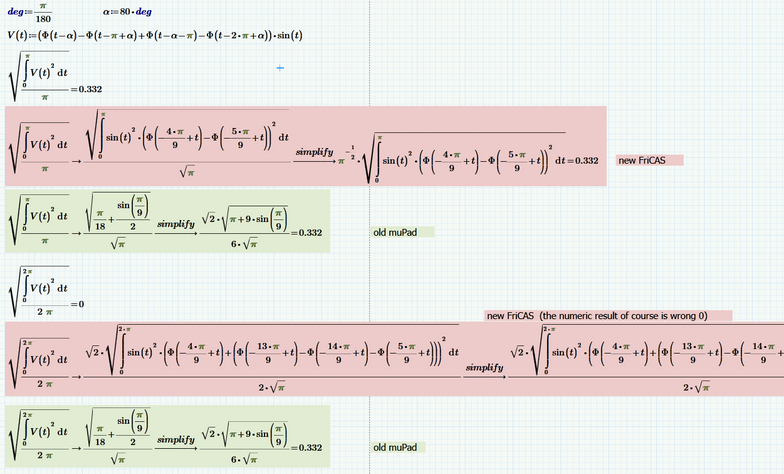
Note that you must use the old legacy symbolics (muPad). It will not work when using the new friCAS.
Worksheet in P6 format attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
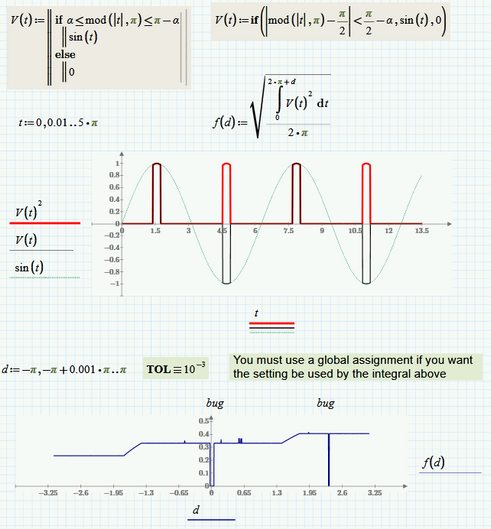
Mathcad and Prime never had much luck with integrals, neither symbolically nor numerical as in your example.
Defining the function in a different way like the two shown in the pic does not help much:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not necessarily restricted to Prime 6, Prime 4 shows the same.
Mathcad 11 too:
The value of TOL has some effect.
As usual, symbolics is right:
How is that in Prime?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How is that in Prime?
Here you are!
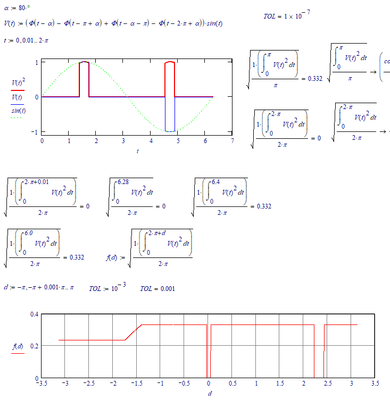
I gave it a try with Prime 6 using the new and future symbolics (friCAS) and the old one (muPad). The new symbolic is not really convincing. The simplification of muPad is (even without using simplify) even more compact than your Maple result 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
you shouldn't square the function containing the Heaviside function but only the function defined in the window created with the step function. See the picture:
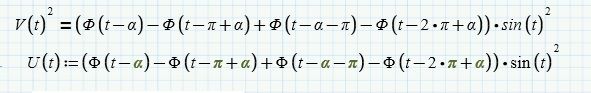
don't square U(t). However, the rms is still zero.....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Squaring the sine 'within' gives you a different function:
with a different symbolic result:
but numerically it's still flawed...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you misunderstood what Francesco meant.
The idea was not to replace V(t) by his U(t) but rather replace V(t)^2 by his U(t).
I am not sure what the benefit of doing so would be, though.
BTW, here is more clearly the deficiency of the new symbolics (friCAS) in Prime when it comes to integration with the Heaviside function with the step inside the integration interval:
We always moaned about Prime would not be developed (or not fast enough). Replacing the very old symbolics engine muPad by a new, more modern one sure is a good a big development step. When we moaned in the past about development, have we forgot to state the direction in which we would like to see development taking place? We did not meant the direction of making things worse!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I misunderstood.
After investigation: The intended method should not make a difference, because PHI only takes on values 0 or 1, and likewise PHI^2 only takes on values 0^2=0 or 1^2=1. Mathcad 11 symbolics still gives the same (correct) answers. Numerically it's still a mess.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

For Fourier analysis, if the signal is f(t)=-f(t+T/2) integral from 0 to pi is OK. Otherwise, we should integral from 0 to 2*pi. Therefore, this bug is sever problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about this approach?
Note that you must use the old legacy symbolics (muPad). It will not work when using the new friCAS.
Worksheet in P6 format attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
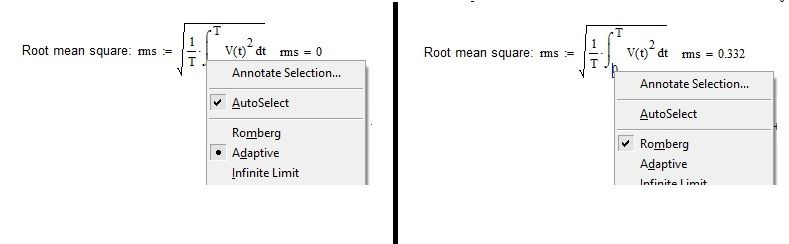
Hi,
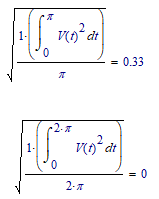
Mathcad 15 gives almost the same results. However, if we change the integration algorithm the result is not null; see photo:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for using time for my question.
In electricel engineering RMS of sin(t) must 1/sqrt(2)=0.7. The denominator is fixed to T, that is a period of fundamental signal, in this case 2pi.