Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
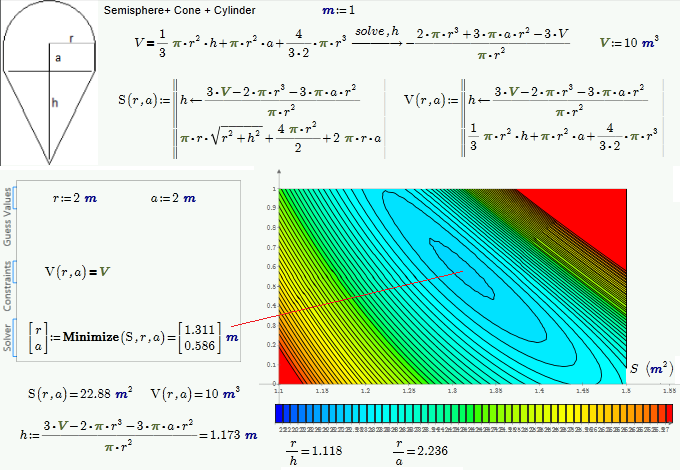
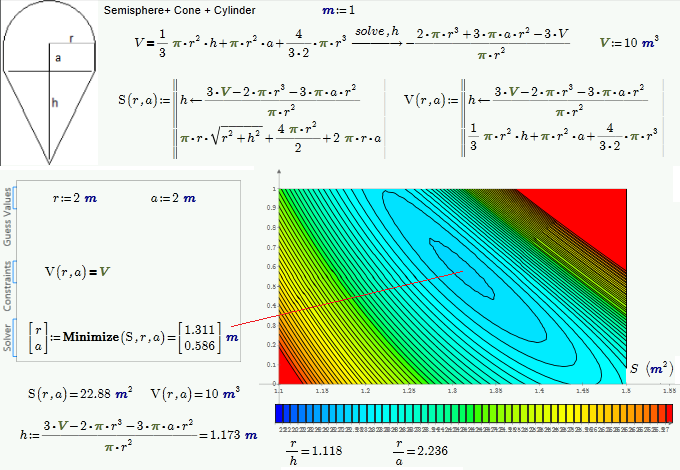
Real and positive root needed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Real and positive root needed
How can I gat a Real and positive root - see the picture and attach (Mathcad 15 and, pardon, Mathcad Prime 2.0)

Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
What problem is wrong?
The last time the discussion went along the symbolic solutions of your cone-semisphere problem which Mathcad is not able to deliver.
But as I see Harvey was dealing with the original problem in your first post and I think his approach of making the functions dependent of the demanded ratio is generally a good one. Next simplification could be to get rid of the generic V and replace it by, lets say,1, as the ratio should not depend on V.
Unfortunately this approach does not help with the symbolic solution of the cone-semisphere.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We can simply remember the solution of this problem - zero, point and three eights:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Result in Web page WolframAlfa is the same in Mathematica 9.See attach....12 roots all contain the imaginary part.I tried different ways to get rid of the imaginary part, but to me did not work.![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
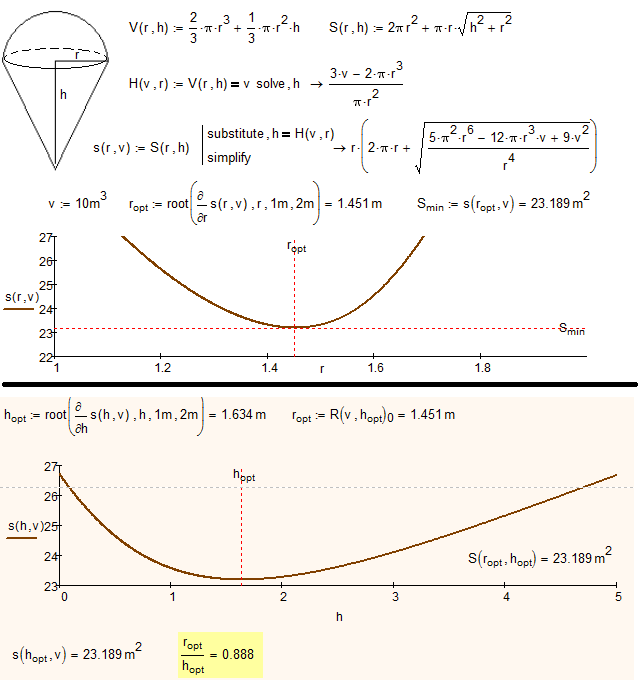
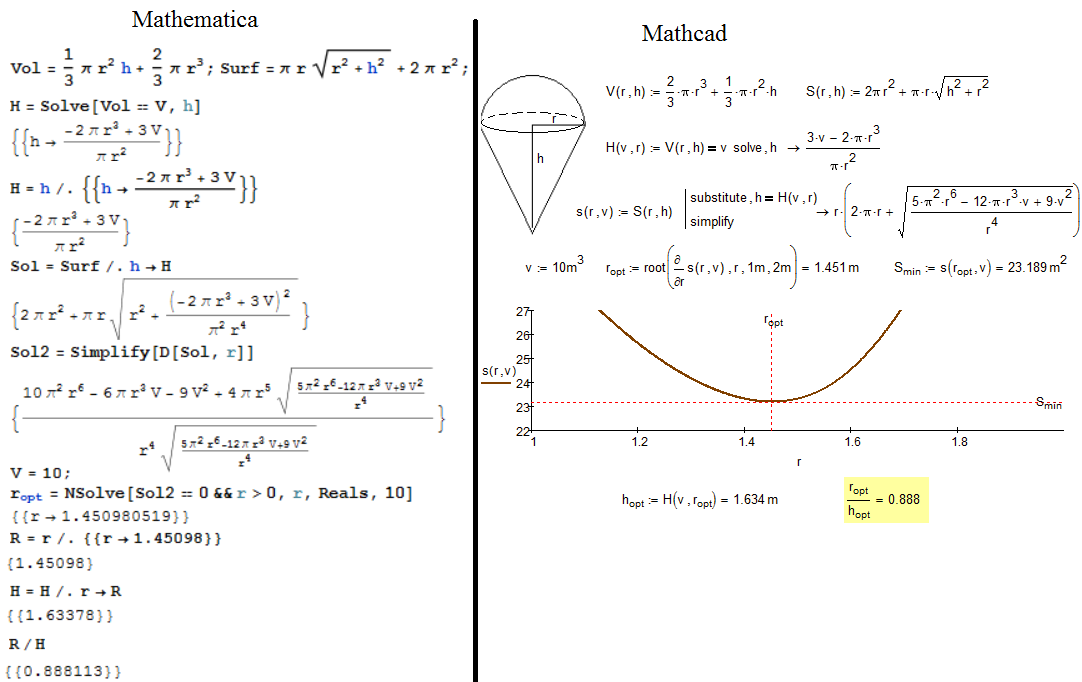
Easier problem for Mathematica, Maple etc:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numerical no problem with Semispher-Cone and Semicircle and Triangle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Compare pleace:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is, in fact, possible to get Mathcad to display a symbolic solution to the cone and hemisphere problem - see attached. Can't see that it's of anything but academic interest though!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK!
And what is it 0.888... in Mathcad?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
OK!
And what is it 0.888... in Mathcad?
Evaluate cot(theta)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov schrieb:
OK!
And what is it 0.888... in Mathcad?
Evaluate cot(theta)
No - ctg(θ)

It is also easy to remember (as 888) - I was born in 1948 (deg), the day was 23 (min). February in this year had 29 days (sec) ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ingenious ideas used in your sheet!
So it wasn't a Mathcad limitation but rather a user limitation ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Ingenious ideas used in your sheet!
So it wasn't a Mathcad limitation but rather a user limitation
And what about a symbolic solution this problem. We must solve not one equation but a system of 2 equetions:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
That's one helluva size ice cream cone, Valery! Is there a particular reason you want a symbolic solution?
Only academical interest and a tool to check Mathcad, Maple, Mathematica etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
That's one helluva size ice cream cone, Valery! Is there a particular reason you want a symbolic solution?
Russian winters. Lots of ice. Very symbolic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
AlanStevens wrote:
That's one helluva size ice cream cone, Valery! Is there a particular reason you want a symbolic solution?
Russian winters. Lots of ice. Very symbolic.
Yes!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
Great solution!
I think one use for this cone-hemisphere problem would be to reduce the rate of melting of ice cream. In that case, minimizing the heat transfer would be the objective, not the surface area. If we assume the air film has a resistance and the cone wrap has a higher resistance, then we can determine a ratio of the resistance at the cone to the resistance at the ice cream top. The ratio of the height to radius increases as this resistance ratio increases. I have a numerical result in the figure. I only did a numerical solution. I also haven't bothered to determine a typical resistance ratio.
I'm not sure which is more fun...working on this problem or eating an ice cream cone!
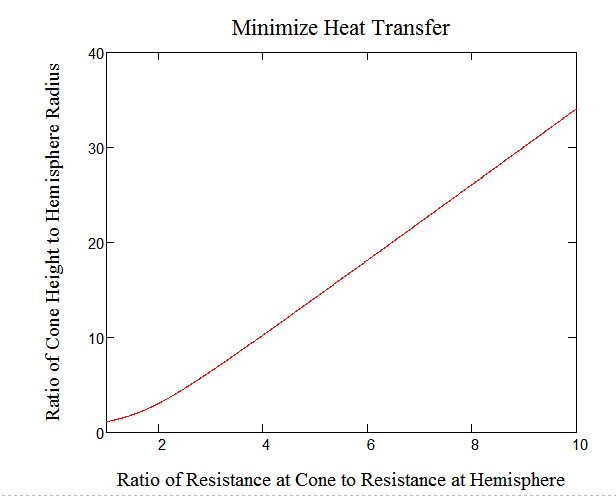
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan and others,
It appears that MC is really particular in how this problem is approached. In the attached file, I changed one statement of Alan's (mine is highlighted). This results in the immediate symbolic result taking a different form, although the results are equivalent. The net result at the end of the worksheet is that the final symbolic result can't be obtained in a reasonable amount of time.
All I did differently was ask MC to do a substitution instead of me doing it by hand.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey,
Yes, the smallest of changes can change the path taken by the symbolic solver - sometimes leading to a dead end. That's why one often needs to play around with the equations a little. Brute force and ignorance can't always be relied on - as I've often discovered to my cost!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
It is, in fact, possible to get Mathcad to display a symbolic solution to the cone and hemisphere problem - see attached. Can't see that it's of anything but academic interest though!
Alan
Sorry, Alan!
The theta in the answer must have an unit not rad/deg but steradian - it must be not a 2D angle, but a 3D-angle! ![]()
We have 2D-angle in same problem but with Area (const) and Perimeter (minimum)!
I never seen steradians in Mathcad-sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- « Previous
- Next »