- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Require real solutions from the symbolic solver
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Require real solutions from the symbolic solver
I'd like to get purely real solution out of the symbolic solver (ie not a product of i) - is it possible to require this? For example solving x^2 +y^2 = 1 for x should return sqrt(1-y^2).
Am I just failing to use assume keyword correctly?
Thanks
Joe
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Joseph Stavitsky wrote:
I'd like to get purely real solution out of the symbolic solver (ie not a product of i) - is it possible to require this?
Sometimes, yes.
For example solving x^2 +y^2 = 1 for x should return sqrt(1-y^2).
Why do you think that sqrt(1-y^2) is "purely" real? Thats only the case if y is real and |y|<1.
Furthermore it would be wrong if MC simply would return that single root as the correct solution is +- the root
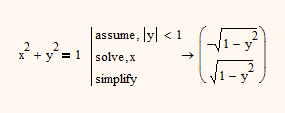
Am I just failing to use assume keyword correctly?
How could we tell if you don't show what you are doing??
Unfortunately "assume" is a pita - it may work as expected but very often it doesn't and it may even be completely ignored in some cases.
So forcing MCs symbolics to avoid the imaginary unit in its results can be quite tricky and is unreliable.
Sometimes the order of the keywords matters and sometimes results look differently if, eg, you use a keyword like "simplify" twice. So quite often its a trial an error type of game.
LT
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Joseph Stavitsky wrote:
I'd like to get purely real solution out of the symbolic solver (ie not a product of i) - is it possible to require this?
Sometimes, yes.
For example solving x^2 +y^2 = 1 for x should return sqrt(1-y^2).
Why do you think that sqrt(1-y^2) is "purely" real? Thats only the case if y is real and |y|<1.
Furthermore it would be wrong if MC simply would return that single root as the correct solution is +- the root
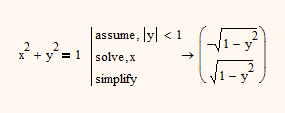
Am I just failing to use assume keyword correctly?
How could we tell if you don't show what you are doing??
Unfortunately "assume" is a pita - it may work as expected but very often it doesn't and it may even be completely ignored in some cases.
So forcing MCs symbolics to avoid the imaginary unit in its results can be quite tricky and is unreliable.
Sometimes the order of the keywords matters and sometimes results look differently if, eg, you use a keyword like "simplify" twice. So quite often its a trial an error type of game.
LT
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
correct on all counts ty





