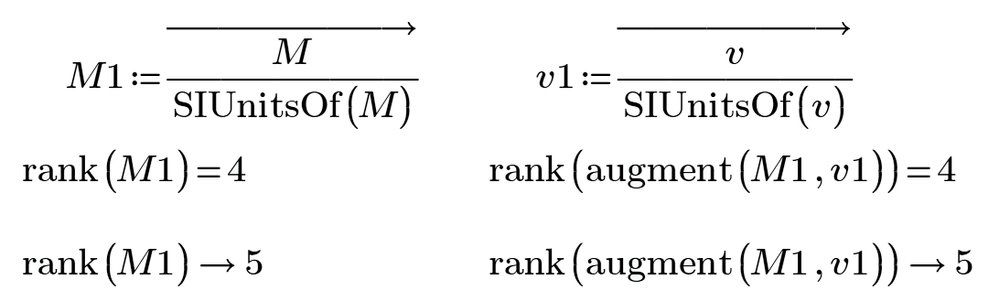Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Rouché–Capelli theorem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rouché–Capelli theorem
See please the attach - Prime 6.
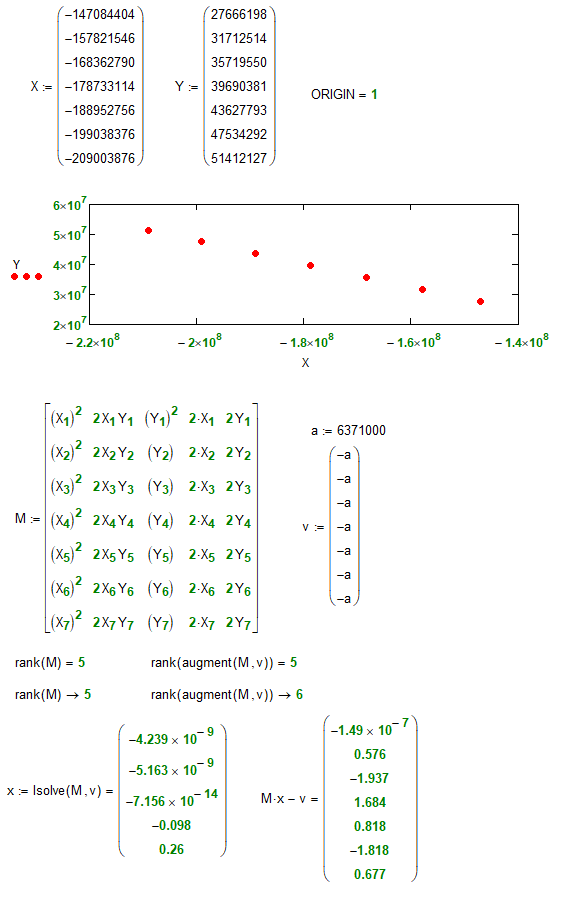
Why in case 1 we have rank = 4
but in case 2 we have rank = 5?
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The theorem syas:
"A system of linear equations with n variables has a solution if and only if the rank of its coefficient matrix A is equal to the rank of its augmented matrix [A|b].[1] If there are solutions, they form an affine subspace of R n {\displaystyle \mathbb {R} ^{n}}
of dimension n − rank(A). In particular:
- if n = rank(A), the solution is unique,
- otherwise there are infinitely many solutions."
In your both your cases the rank of the matrix and the augmented matrix are the same. But in case1 that rank is 4, unequal to the number of equations, so there are infinitely many solutions.
In the second case you picked one solution, so the rank equals the number of equations.
The discrepancy is probably caused by the larger difference in X and Y values for the second case 2. I guess in case 1 you loose precision due to the large numbers all close together.
The numeric rank function is limited by numeric precision. I get this from the symbolic processor:
What does the symbolic processor in Prime say about the rank?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The theorem syas:
"A system of linear equations with n variables has a solution if and only if the rank of its coefficient matrix A is equal to the rank of its augmented matrix [A|b].[1] If there are solutions, they form an affine subspace of R n {\displaystyle \mathbb {R} ^{n}}
of dimension n − rank(A). In particular:
- if n = rank(A), the solution is unique,
- otherwise there are infinitely many solutions."
In your both your cases the rank of the matrix and the augmented matrix are the same. But in case1 that rank is 4, unequal to the number of equations, so there are infinitely many solutions.
In the second case you picked one solution, so the rank equals the number of equations.
The discrepancy is probably caused by the larger difference in X and Y values for the second case 2. I guess in case 1 you loose precision due to the large numbers all close together.
The numeric rank function is limited by numeric precision. I get this from the symbolic processor:
What does the symbolic processor in Prime say about the rank?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Luc!
I have forgot about symbolic solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think this proves my guess:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SLAE with 5 unknowns and 7 equation - I have been waiting for an answer already half a day. Do I still have to wait?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thought you know by now that Prime is slow.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator