Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Simple Vector Question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simple Vector Question
Hi, All --
I have what I fear is a too-simple question. For some reason, I am having a real mental block figuring it out, though. Say I have some vector in R3 (x, y, z). I would like to find a vector orthogonal to this one. The obvious solution is (1/x, 1/y, -2/z). However, this blows up if one or more of the components of the original vector is zero (i.e., if the vector lies in a plane defined by the global coordinate system).
We have a way to handle this is an ad hoc fashion (if statements), but it seems to me that there should be some slick linear algebra that we could emply to solve this problem in a more elegant way, but it currently escapes me.
Thoughts?
Thanks in advance.
Matt
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure but I think you will run into some kind of singularity or error with any simple formula.
See attached two very different ways to get a normalvector - both have its drawbacks.
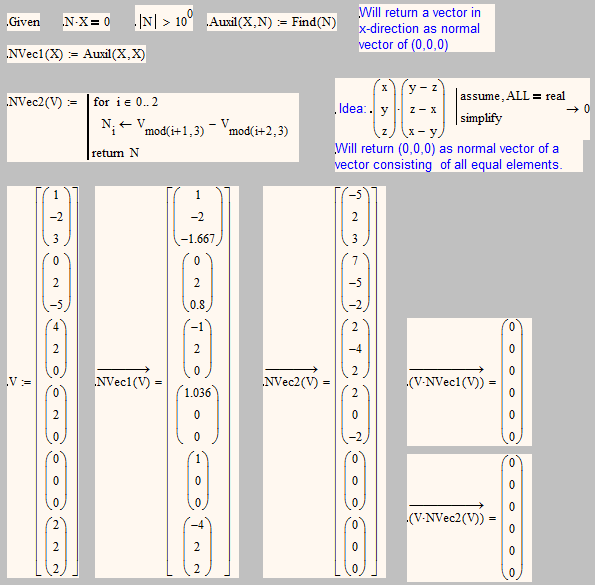
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a bunch -- I like that "shorter" idea, Werner -- it allows us to trap only one potential error (i.e., x=y=z) rather than several. It's not perfect, but much faster than our alternative. We're actually just testing some calculations in Mathcad but then implementing them in a scripting language in a different piece of software. SInce we will need to perform this calculations many millions of times, speed is of the essence.





