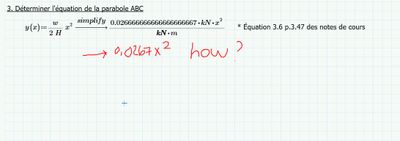Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Simplify equation 4 decimals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simplify equation 4 decimals
Hi, I would like to have the answer to this very simple equation with only 4 decimals. Also, is there a way not to show the units ?
Thank you
Camille
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
-
Mathcad Usage
- Tags:
- simplify
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can (but it's "cheating"!)
The attached file shows you how. There are three varieties of "y(x)" below yours. The yellow one works just fine, you don't have to simplify every function. The middle (grey) function works. The pink function works BUT it will lie to you because the units won't balance, because 0.0267 is only valid because it requires all lengths to be meters. That function will result in y(x) being reported in meters squared.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can (but it's "cheating"!)
The attached file shows you how. There are three varieties of "y(x)" below yours. The yellow one works just fine, you don't have to simplify every function. The middle (grey) function works. The pink function works BUT it will lie to you because the units won't balance, because 0.0267 is only valid because it requires all lengths to be meters. That function will result in y(x) being reported in meters squared.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank's a lot !!
Have a great day
Camille
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
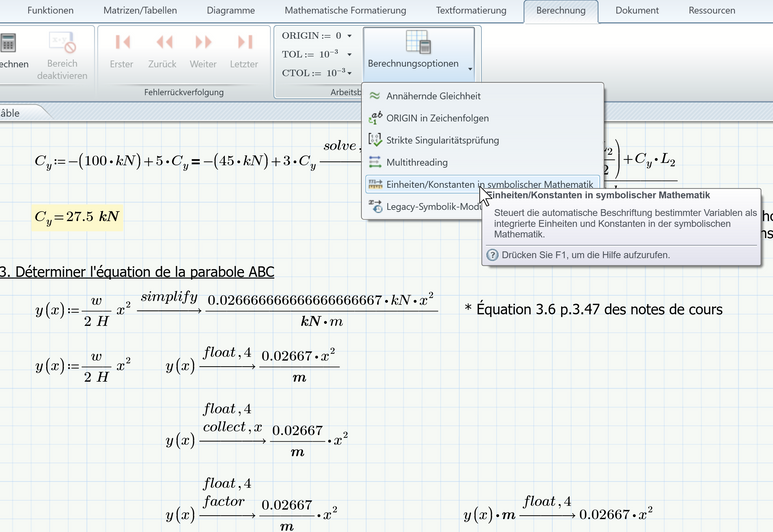
As you are working with units you should not suppress the correct unit when evaluating expressions. But you sure can do something against the too many decimals and the fact, that the symbolic engine does not cancel the unit kN.
The symbolic does not know anything about units and autolabelling in Prime is rather faulty, so some kN are seen as unit and some as variable. Thats the reason why in the symbolic evaluation the kN are not cancelled. There is an option which sometimes can help in this situation - turn on "Units/Constants in symbolic calculation" as shown in the picture. This will allow the cancelling of the unit kN.
To display less decimals you might use the "float" modifier. But it should be handled with care, as it does not only apply to the display of the result but it applies to the whole calculation! Thats the reason I first assign the expression to y(x), preserving full precision and then I evaluated y(x) in a separate region with just 4 significant digits.
You may use the "collect" or the "factor" modifier if you like the displayed result better.
If you really don't wan to see the unit 1/m you may simply evaluate y(x)*m as shown in the lower right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank's for the tips. It works just fine 🙂