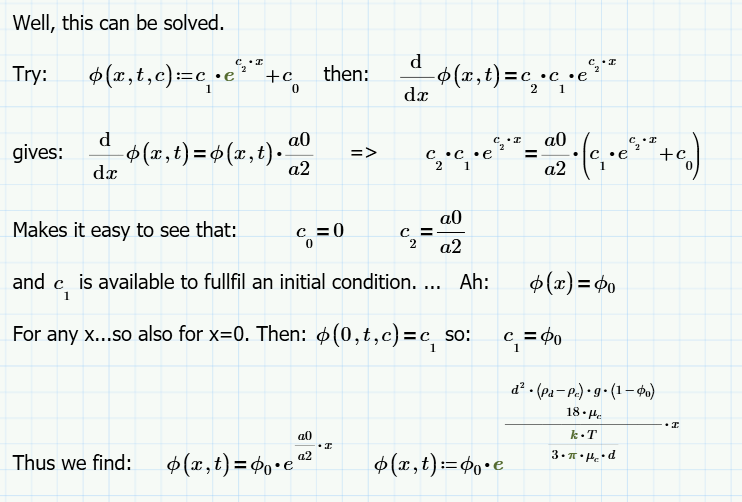Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve non linear second order differential equation with initial and boundary condition
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve non linear second order differential equation with initial and boundary condition
Hi,
I am trying to model the sedimentation of spherical colloidal suspensions. For that, I need to solve the differential equation (check image file). I am attaching the mathcad file and the original paper. What I want is to plot volume fraction (phi) as a function of height (x) at a certain time (t) (Something similar to figure 3 in the paper). I would greatly appreciate the help.
Regards
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
It should be convenient to install Mathcad 15 since it offers the possibility to solve partial differential equations, with the "Pdesolve" operator inserted in a solution block (there is an example), and of which Prime is deprived.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm afraid PDEsolve (real Mathcad) will not help.
My results, analysing your equations:
Unfortunately, the coefficient of x in the exponent is positive, and large (about 23 million /m), which means that the function goes steep to infinity...
I don't suppose this accurately models your phenomenon...where did I, or you, go wrong?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
There is a slight confusion with your solution. The equation 4 that I had written is a modified version of equation 3 and is a boundary condition. Therefore I don't think phi (x,t) is independent of t. The derivative of the expression may be 0 at the boundaries but not everywhere else. Volume fraction will change along the solution length as sedimentation takes place with time. I am attaching the mathcad file with my comments. Take a look.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess you're right, I mistook the "x ∈ {0, xmax}" (= just 0 and xmax) for an "x ∈ [0, xmax]" (=the entire range from 0 to xmax).
Sorry about that.
Other than that, Werner already explained that PDEsolve is not available in Prime, if you want to use PDEsolve you'll have to use (real) Mathcad.
{ Note that as a licensed user of Prime you're allowed to install and use Mathcad 15 on the same machine. You can use the very same license file that you used for licensing Prime to license the Mathcad 15 application. }
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thanks. Let me try it in mathcad 15. I have never really used it. I'll post again if I have issues.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You'll love the speed (once you've unlearnt the Prime habits).
Be aware that (real) Mathcad does not like units with its solvers, so you'll have to set up the stuff unitless (= you're advised to express every value in standard units).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It may not all be correct, but this is what I get in Mathcad 11. I wonder if it's how you'd expect it to be:
The file is attached. You should be able to open it in Mathcad 15, and the part that is shown in the picture here should be similar.
The symbolics manipulations may not work in Mathcad 15, but you should be able to make them work with some tweaking.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Sorry for the late reply. I am able to open the file that you sent me. But some how I am not able to see any of the evaluation or symbolic results. There is some issue with viewing mathcad 11 file in 15 (see attached). I have written everything in mathcad 15 but it is giving me an error when I do the pdesolve.
It says "This value must be a function, but has the form: Unitless." I am not sure why I am getting it. Can you please take a look at it. (File attached)
Also is there any way to plot phi vs x for a particular time say after 20 hrs. That will give me a better idea. Thanks for the help.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As demonstrated by Image # 1, you didn't calculate. Open my Mathcad 11 file, scroll to the bottom, and press the F9 key on your keyboard once.
That should solve most, if not all of the issues.
(I usually work in the mode where the sheet does NOT calculate automatically, too keep manipulations editing quick...)
Don't hesitate to come back if there are problems left.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Luc. F9 sorted that particular problem.
The 3 d plot is slightly confusing. How can I plot phi vs x for a particular time t. The particle volume fraction should be higher at the base (x=0) compared to the rest of the solution after sedimentation. Please see attached image. If I can get a profile similar to that, then I think the model is a success. Thanks a lot for the help.
Another question is if I want to do this in prime can I use numol instead of pdesolve.
Regards,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Luc. F9 sorted that particular problem.
The 3 d plot is slightly confusing. How can I plot phi vs x for a particular time t. The particle volume fraction should be higher at the base (x=0) compared to the rest of the solution after sedimentation. Please see attached image. If I can get a profile similar to that, then I think the model is a success. Thanks a lot for the help.
Another question is if I want to do this in prime can I use numol instead of pdesolve.
Regards,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I should think that the attachment of my Mathcad 11 file today shows a plot of phi versus x at tp=20 h.
I was surprised that I got a result from pdesolve so quickly. Next I was surpised by the result itself, showing that the particle concentration at any given time would fluctuate over height, and realised that it doesn't match what the authors of the article found. That's why I hinted that I may have made a mistake somewhere. The authors indicate at some point that the numerical approximation is tricky. Maybe pdesolve is fooled and/or not the right tool for this problem.
As for numol: I have little experience with pdesolve (I can remember having used it only 1 time in the past 10 years, and that was somewhere in the past few days...), much less experience with numol. I just read the description, and it seems worth a try. Go ahead and share your results. But don't expect completely different results. It may very well be that the numeric algorithm underlying both pdesolve and numol are equivalent, if not the same.
Success!
Luc
P.S. Found one error, see attachment for correction.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thanks. Just saw the plot.
What I am noticing is that the phi never reaches phi eff.max near the base. it is always around phi0. If I increase the phi0 value (lets say by 3 orders of magnitude or more), then it gives me an error saying that there is a singularity. I also noticed in the pde that the (1-phi (x,t)/phi effmax)^2 is missing. Maybe that can make a difference.
I don't know much about pdesolve to comment on how it might be getting tricked to give the wrong answer. Do you know why it can happen.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Never mind. You replace it by a1. It must be due to something else.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numerical instability. Small differences in numbers giving large differences in results.
Example: working with x close to 1 on the function 1/(1-x)...
Some numerical methods are more stable than others.
That's one of the reasons why my preference always is to find a symbolic solution first. In the case of your problem I don't see a way to that yet.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
The problem here is if I increase the volume fraction phi 0 (see attachment), it returns an error. Is there any way around this? The paper talk about breaking the pde into coupled system of ODEs. They used matlab though.
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the info on pdesolve in mathcad 11:
"Pdesolve(u, x, xrange, t, trange, [xpts], [tpts])) Returns a function or vector of functions of x and t that solve a 1-dimensional nonlinear PDE or system of PDEs. Values are interpolated from a matrix of solution points calculated using the numerical method of lines."
And this is the info on numol in Prime:
"
- numol(x_endpts, xpts, t_endpts, tpts, num_pde, num_pae, pde_func, pinit, bc_func)
Returns an [xpts x tpts] matrix containing the solutions to the one-dimensional Partial Differential Equation (PDE) in pde_func. Each column represents a solution over one-dimensional space at a single solution time. For a system of equations, the solution for each function is appended horizontally, so the matrix always has xpts rows and tpts * (num_pde + num_pae) columns. The solution is found using the numerical method of lines.
"
So numol will solve a matrix of points using the same 'numerical method of lines' that pdesolve uses to create a matrix and allow the result to be used as a function (by interpolation), similar to how rkfixed and odesolve are related for ODE's.
I can choose between 4 different interpolation methods for pdesolve in mathcad 11.
Sounds like you should be able to produce the very same 3D graph in Prime.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
I have tried to use numol in mathcad prime. Just wanted to see whether we get a different result. However, I am getting an error. I need some help with it (file attached).
Also from the paper , hindered settling velocity u(phi) is positive in the upward direction (direction opposite to settling). Kindly check attachment.
That may give a different result. For the time being I haven't made any changes. Just wanted to see what I get with numol. Thanks a lot for the help.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just above calling numol, you define bc_funct(t), in which you call the function bc() twice. But you call bc() with just one parameter, while it is defined (right above there) to have/require two parameters. That is what the error message, attached to the matrix M (below calling numol), is complaining about.
(Providing clear and to-the-point error emssages was never a strong point of Mathcad, and Prime didn't improve much on that point.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
It is giving me a different error now. "Matrix is not valid because boundary condition is not valid". This is the same boundary condition used in pdesolve. Also rhs has 5 different parameters in it. Would that not affect it?
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I bet Prime doesn't like the way you set up your init() and bc() functions, using a programming bar.
Anyway. I experimented a little with numol in Mathcad 11, and got this:
Note that I used the very same values as for pdesolve, a few days ago.
What struck me is the fact that phi goes negative here, which I attributed to the fact that your boundary conditions aren't exactly included (notice how bc_func only specifies 0's). I guessed they should be better added as a form of PAE (see help description) but so far have been unlucky in using numol with a PAE construct. And I'm not the only one. I searched this forum, and found no successful examples.
Then I experimented with more spatial resolution: changed nx from 25 to 250. The result is that the pdesolve solution now goes negative like the numol result shown above, but the numol result with that same spatial resolution stays mostly positive.
I hope you can port the implementation to Prime and make it work there. My Mathcad 11 file with pdesolve and numol is attached.
Success!
Luc