Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solver cannot find solution even though one exists - Mathcad Prime 3.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solver cannot find solution even though one exists - Mathcad Prime 3.0
I've been working on a problem to determine the formulas for two sinusoidal fibers that are tangent to each other, as shown in the attached picture. I've already pursued this problem with the GRG Solver built into Microsoft Excel and determined that there are multiple solutions, but I wanted to transition to Mathcad. After entering the governing parameters and constraints I found that the solver functions if my guess is the same as one of my solutions, but if I change a guess (specifically for A1 or D1 in the file) it will not solve.
I don't know if I'm doing something wrong with Mathcad or my constraint equations, or if I'm just experiencing limitations of the solver.
I attached my Mathcad file with the most trivial solution entered, as determined by hand. Slightly changing A1 from 1 to 1.1 causes the solver to fail.
Can anyone provide any insight on this? Thanks in advance.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your function definitions will only use the current, initial values of x1, xt, etc.
To make them work with the changed/iterated values of the solve block, you must make them arguments of those functions.
E.g.
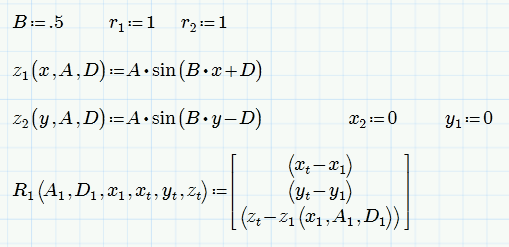
And this functions and variables should be defined before the solve block - they are neither guess values for the solved for variables nor constraints.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I did the vector math out by hand and used the resulting equations instead and now it works. I'd still like to know why the setup I was using before did not work, but I can now proceed with my problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your function definitions will only use the current, initial values of x1, xt, etc.
To make them work with the changed/iterated values of the solve block, you must make them arguments of those functions.
E.g.
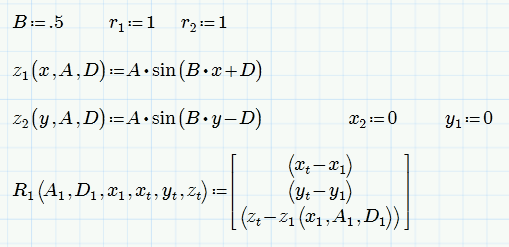
And this functions and variables should be defined before the solve block - they are neither guess values for the solved for variables nor constraints.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks! It works like a charm. And thanks to Luc for demonstrating the entire solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you do as Werner indicated, you should get something like this:

And see that it works for A beyond 1.1.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the result found for a guess value of A= -1.11:

And additionally changing the guess value for x1=2 gives:
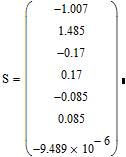
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I see 7 variables to solve for but only 5 equations!
So there still are some degrees of freedom.





