Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving for variables - 3 equations; using newton's method & Jacobian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving for variables - 3 equations; using newton's method & Jacobian
Hi there,
I am trying to solve 3 equations with 3 variables. The form of the equation is as follows:
F(x,y,z,t) , G(x,y,z,t) and H(x,y,z,t). I'm attaching mathcad file.
When t is known or fixed, say t=2 or t=3 etc, I can solve these three equations. See attached for the functions and t.
But, I don't know how to generalise it, i.e. when t has a range of values, say t = 1,2,3 and so on. I would be glad if someone can look into this program and help me. Once I know how to program it for the this case, I can then perhaps do it for nonlinear case.
Thanks,
Ashehad
- Labels:
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Valery,
I managed to visit the site you mentioned. However, I still have the same problem. i.e. How to modify the program so that it can give all the solutions corresponding to different values of t. i.e. I'd like to have solutions in an array. In other words, referring to the file I attached, I'd like to have x(t), y(t) , z(t) for t say from 1, 2,3...100.
I want to avoid typing each value of t and then noting its solution. Can the program be modified? e.g.by including loops.
Thanks,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alan,
Thanks a lot indeed.
Cheers,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alan,
The short program which you wrote is fine. Works well. However, I would like to know if it could be improved , i.e. At the moment, the initial vector, "x" for every "i" is same. Could it be improved such that the initial vector for "x" for "i+1" is the final vector for "x" for "i"?
Thanks,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ashehad Ali wrote:
Hi Alan,
The short program which you wrote is fine. Works well. However, I would like to know if it could be improved , i.e. At the moment, the initial vector, "x" for every "i" is same. Could it be improved such that the initial vector for "x" for "i+1" is the final vector for "x" for "i"?
Thanks,
Ashehad
Yes, with just a minor reordering - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks once again, Alan.
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alan,
Just wanted to check with you the procedure to solving for variables for the nonlinear case. Actually, I'm solving two nonlinear equations with two variables. We hope to use the same method as we used in the linear case. Just letting you know that we solved a nonlinear equation of the similar form, which had a unique solution. In that case, the solutions when plotted were a curvilinear. So we expect the solutions of two nonlinear equations to have unique solutions too and behave curvilinear. See the file attached.
Attached, is the file which I'm currently working on. I hope the procedure is okay. Could you please check?
Thanks,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See modifications attached - they might help. However, your functions are prone to singularities which will give any numerical solver problems under some circumstances.
Alan
Edited to replace attached worksheet with one with an additional function.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alan,
Thanks. Yes, there do exist singularities, unfortunately. Is it possible to avoid these singularities? I.e. Can we force x>0 and y>0 all the times?. The parameters "a" and "b" are positive always. Actually, x and y represent production rates, therefore have to be positive always.
I tried solving similar form when the function had only one variable, i.e. when the function was just in terms of "x" and "a". Precisely, when it was "x/1-exp(-ax)) - HSj". To solve this, I used newton's method too for the same values of HSj as given in the table. But for, "x=0" we note the function is undefined. Hence, I used Taylor's series, expanded the function about zero and redefined the function as "1/a" for "x=0" and it worked fine. So this is how I managed to avoid the singularity but the x values which I got was "negative" for some values.
Thanks,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You know what collab,
Plug your real non-linear system in this forum.
If you have a function, what is the point to Taylor ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jean,
I'm just explaining how I managed to solve a single equation of the similar form when it just contained "one variable". The second paragraph of my last message is about that.
Now, in the case of 2 equations and 2 variables, we do have similar problem. You will note when going through Alan's latest file that the function for two variables "g0" and "g1" are undefined at "x=0" and "y=0". See Alan's last file that he posted. There are singularities for this case as he suggested.
Thanks,
Ashehad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ashehad Ali wrote:
Hi Alan,
The short program which you wrote is fine. Works well. However, I would like to know if it could be improved , i.e. At the moment, the initial vector, "x" for every "i" is same. Could it be improved such that the initial vector for "x" for "i+1" is the final vector for "x" for "i"?
Thanks,
Ashehad
This is in fact your fourth switch for the same "non-linear" project and you might have missed some of my NL examples. By themselves, as noted by Fred, Given/Find/Minerr is a non-linear. The Mathcad non-linear has been tested up to an 8 x 8 NL and found superior to dedicated NL $ software ! Your idea of seeding Xi seems either non realizable or otherwise very difficult. The seeded root scanner works charmingly well for one variable. You could submit a visible project to other forum like the Maple, Mathematica, Matlab ... because up to your last visit, your project is limited to Mathcad 14 and higher versions and thus limits the audience. My point here is that eventually your project may be ill posed on the mathematical basis and on the Mathcad usage as well , do you get my point ?
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
... Your idea of seeding Xi seems either non realizable or otherwise very difficult. The seeded root scanner works charmingly well for one variable. You could submit a visible project to other forum like the Maple, Mathematica, Matlab ... because up to your last visit, your project is limited to Mathcad 14 and higher versions and thus limits the audience. ...
jmG
jean,
I've attached an M11 version for you. It's possible that Ashehad is just interested in evaluating the efficacy of this particular method, as he displays the values at all iterations. If he's only interested in the solutions then he might well value your alternative suggestions.
Alan
NB The example equation set he provides in the attached is, of course, linear.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>NB The example equation set he provides in the attached is, of course, linear.< [Alan]
___________________________________
Alan,
Thanks for the reading, for the given system the solution is unique.
In the sense of the original post about solving with changing 't'
and solving again, the solver does not change. In the sense of
"non-linear" about any of the x, y, z ... solve linear and root
for whatever each argument may be solved for .
1. Four threads for no real problem,
2. Nothing to pass to other CAS !
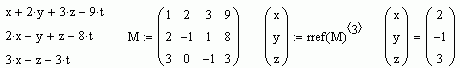
Cheers, Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan Stevens wrote:
jean Giraud wrote:
... Your idea of seeding Xi seems either non realizable or otherwise very difficult. The seeded root scanner works charmingly well for one variable. You could submit a visible project to other forum like the Maple, Mathematica, Matlab ... because up to your last visit, your project is limited to Mathcad 14 and higher versions and thus limits the audience. ...
jmG
jean,
I've attached an M11 version for you. It's possible that Ashehad is just interested in evaluating the efficacy of this particular method, as he displays the values at all iterations. If he's only interested in the solutions then he might well value your alternative suggestions.
Alan
NB The example equation set he provides in the attached is, of course, linear.
Thanks Alan,
Nothing has changed, the system is linear, it solves immediately. If ' t ' varies as integers in simple progression, the setup is as simple as indicated in "sol". It ' t ' does not vary in that kind of progression and each ' t ' is anything, the process can be isolated to suit but it can be generalised too. But for that kind of exercise, the collab must have some project that justify the time to develop. What I mean is that it's too much asking to spend time for home project that may have no use though it is easy to see it as useful, very useful. Just surprised that in 10 years and > 100000 visits and 1000's solving done, this kind of "solving" arises only recently. What is Newton & Jacobian doing in there ? Again: non-linear solve via Given/Find/Minerr and not so easy ! For the two big images, too late for them to be executable work sheet style ... most of the stuff replied is collected and gone in image for some beginners to code and old Mathcaders to shop for what they might have missed as part of the tool box.
On the same proposal that ' t ' is made variable, the project can work in interchange mode, i.e: interchange any two row or any two cols or in mixed mode. A complete setup is very recent for collab Loi. Fishes don't grow wings so fast to jump from rivers to rivers like that demand here had switched 3 times for a total of 4 dispersions. No wonder why you and me are the two left collabs chasing dragon flies instead of fish . There is a simple way of addressing this hypothetical project for any values in "N", i.e: get it indexed generated symbolic and fill-in the blanks. That was done in the past too and filling the "N" array can be done in many ways.
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ashehad Ali wrote:
Hi there,
I am trying to solve 3 equations with 3 variables. The form of the equation is as follows:
F(x,y,z,t) , G(x,y,z,t) and H(x,y,z,t). I'm attaching mathcad file.
When t is known or fixed, say t=2 or t=3 etc, I can solve these three equations. See attached for the functions and t.
But, I don't know how to generalise it, i.e. when t has a range of values, say t = 1,2,3 and so on. I would be glad if someone can look into this program and help me. Once I know how to program it for the this case, I can then perhaps do it for nonlinear case.
Thanks,
Ashehad
I don't understand your proposition [don't worry , I don't have either !]. Your proposition is bi-equivoke in the sense that your first attempt a linear solve in terms of many methods. The last such linear method "rref" is not commonly used, though it introduces to solving 3 planes in the space. Next you switch your proposition to generalize the "non-linear case" . At this point, the non-linear case switches to "quadrics", thus involving the symbolic solve for 'z' while maintaining the full meaning of the quadric. It is then at this point that your proposition is rather confusing in term of the meaning of the quadric wrt to the parameter 't'. What I'm saying is that while the linear case is rather simple and understandable, the switch to the non-linear case might very well deviate from the mathematical meaning and its representation. In short: I have no background in such extension of the "quadrics"with variable parameter.
Cheers, can't help. [jmG]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>But, I don't know how to generalise it, i.e. when t has a range of values, say t = 1,2,3 and so on.<
_______________________________
Don't understand the ranging of ' t '
Can you propose more examples





