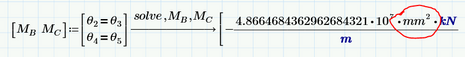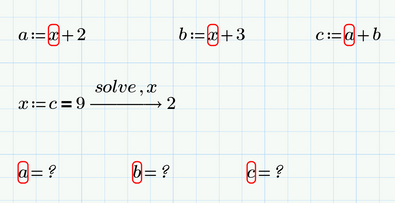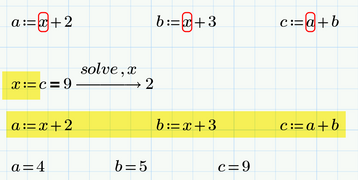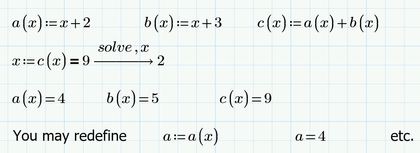Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving with several unknown variables
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving with several unknown variables
Why can't MathCAD solve this equation? It obviously works after simplifying it manually first as shown in the last step. But how can i get MathCAD to do it in the previous step?
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, I think I see the problem. You're trying to have the symbolic solver find m.Rd and you are using units. You should be aware that the symbolic solver does not know units, it treats each unit as an undefined variable. Prime's numeric processor knows, and can transform units as required, but the symbolic solver does nothing with/to them In some cases, depending on the equation, they will cancel out, and then it does not hinder the symbolic processor...
Attached is a different approach, using the root function (Prime 4)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem might occur because you are using a variable named delta, that is undefined. Mathcad assumes that it's the delta function, which requires an argument...
You can change delta to be a variable, by setting its label (see the ribbon) accordingly.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried changing delta to variable, replacing it with an other letter and even defining it as "1".
But nothing works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is the error message that you get from the first symbolic 'solve'?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This variable is undefined. Check that the label is set correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, I think I see the problem. You're trying to have the symbolic solver find m.Rd and you are using units. You should be aware that the symbolic solver does not know units, it treats each unit as an undefined variable. Prime's numeric processor knows, and can transform units as required, but the symbolic solver does nothing with/to them In some cases, depending on the equation, they will cancel out, and then it does not hinder the symbolic processor...
Attached is a different approach, using the root function (Prime 4)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So you are saying that it's pure luck when the solver get units right like in this example?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Rafael1 wrote:
So you are saying that it's pure luck when the solver get units right like in this example?
Absolutely! The symbolics engine doesn't understand units, so if it comes out right it's a happy accident. At first look in your example the units look wrong; but you got lucky:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does the root function always work with units?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Rafael1 wrote:
Does the root function always work with units?
"root" is a numeric function. Mathcad numerics deal properly with units.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Mathcad 11 root is not per se a numeric function:
I haven't found examples of Prime (trying) to use root symbolically...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 15 and also Prime will not accept the 2-argument flavor of "root" but insist on using the 4-argument form. There is no logic in doing so as the symbolic evaluation of "root" does NOT require the function values of the end points of the interval to be of opposite sign and will happily return all roots within that interval.
What hast changed concerning symbolic evaluation are at least two things:
1) We cannot evaluate a solve block sybolically
2) We cannot copy a symbolic evaluation inside a program
Mathcad 15:
Prime 5:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That explains why I did not find examples in the help files using the root function symbolically. The preferred method is to use the solve keyword.
What happens if you set the two range parameters wrongly, like 0, 2 (does it find one root...) or -1, 1 (no roots) ?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
That explains why I did not find examples in the help files using the root function symbolically. The preferred method is to use the solve keyword.
What happens if you set the two range parameters wrongly, like 0, 2 (does it find one root...) or -1, 1 (no roots) ?
Luc
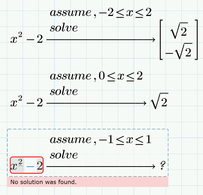
In case of interval [0;2] both MC15 and P5 return correctly just the one solution in this interval.
In case of [-1;1] only P5 fails with no solution found. MC15 strangely switches into float mode and returns both solutions. Only when start and end value are the same, MC15 fails, too.

The very same behaviour is shown by the symbolic "solve" in conjunction with "assume":
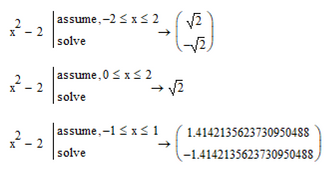
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11's symbolics knows the bracketed root function, but:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Other than that, your equation is indeed simple. Here's how Mathcad can solve it fully symbolically:
Note that delta is not part of the solution, so can be any value that does not lead to (other) problems.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your problem is basically that you define variables using an unknown, then you solve symbolically for this unknown and then you expect all those defined variables magically have their appropriate value based on the now solved for variable.
Thats not the way Mathcad works. It will never go back to a variable definition and insert a value for a variable which was calculated or assigned later. If you want this to be done, you have to define a function instead of a variable.
Her is a simplified version of your problem as I understand it
and her a three possible solutions/work-arounds:
1) Simply assign the solved for value to the appropriate variable and repeat/copy the variable definitions which will happily use the calculated value now.
2) Turn your variable definitions into functions as this is the mathematical construct which changes its value depending on one ore more input arguments
3) Do without the symbolic solve and use a numeric solve block instead. Note the picture below is erratically missing a guess value for x (we don't get an error because x was already assigned a value before in my sheet)!. Note that you have to "find" all variables which depend on the unknown, even though you might not be interested in all of them