Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Stability of Offshore Platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stability of Offshore Platform
Hello all,
Tonight I am attempting the below problem:
The given correct answer is given as 14.49m for the centre of gravity from the keel of the platform i.e. KG=14.49m
I have so far approached this as follows:
I.e. the transverse Gravity to the Metacentre is equal to the Keel to the centre of Buoyancy + Centre of Buoyancy to the transverse Metacentre - KG.
I.e. KG=KB+BMT-GMT
I have also worked on the assumption that:
i.e. BMT is equal to the transverse second moment of the water plane divided by the underwater volume. I've also assumed that the KB is half the draft.
Further I have assumed that as the cylindrical columns are at the waterplane, the second moment of these areas will be about a circle and can be calculated as:
i.e. Pi * diameter to the power of 4/64.
I have carried on as below.
I think that I have calculated the underwater volume correctly and the second moment for one column correctly. I am not sure how to equate the total second moment for the total waterplane i.e. all 8 columns. I am sure it is not as simple as multiplying by 8 as I have done?
Further, I believe that if KB is actually T/2, then BMT would need to be a negative value which is unlikely for the metacentre to be beneath the centre of buoyancy as the metacentre is essentially the point at which the structure will rotate about when heeling either way. In fact the more I think about it the more I believe this must be impossible. So perhaps the KB value needs to be obtained another way than by assuming it is at half the draft?
Any help warmly welcomed.
Cheers,
Andy
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to find the metacenter. This requires you to track the center of buoyancy as the platform tilts.
You owe me!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So Obviously I am still working through this.
So far I have managed to work a proper method of calculating KB using Morrish's formula:
This I can believe is more realistic as most of the underwater volume is at the base of the structure.
I also realised that I had an error in my units so now the area of the waterplane should be correct.
I have also looked at refining my approach to second moment of the waterplane as below but am not convinced this is correct.
So basically I am still stuck and open to help/ suggestions.
Cheers,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you spell out the names of all the terms? The math to solve this problem is easy, but I have no idea what most of the terms you are using mean.
What I am familiar with is that the center of gravity needs to be below the center of buoyancy in order to be generally stable and for the center of buoyancy to move in the direction of tilt to remain stable.
I have no idea what GMt is and no idea what KG is. They aren't labeled on the diagram, so it is harder to guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The terms relate to:
KB = Distance from keel to centre of buoyancy
BMT = Centre of Buoyancy to transverse Metacentre
GMT = Centre of Gravity to transverse Metacentre
KG = Keel to Centre of Gravity
T = Draught
J = Generally used as second moment of area
V = under water volume
A = Area (of waterplane)
X = I generally use for distances
Think that is it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One note, I do not know for Offshore Platforms but for a ship B (centre of buoyancy) does not need to be above the centre of gravity (G).
The normal metacentric situation for a ship is the centre of buoyancy is below the centre of gravity. As the ship heels, the centre of buoyancy indeed moves as the underwater volume shape changes and generally B stays beneath G and the ship will self right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy Wibroe wrote:
One note, I do not know for Offshore Platforms but for a ship B (centre of buoyancy) does not need to be above the centre of gravity (G).
The normal metacentric situation for a ship is the centre of buoyancy is below the centre of gravity. As the ship heels, the centre of buoyancy indeed moves as the underwater volume shape changes and generally B stays beneath G and the ship will self right.
The situation you describe above has an inherent danger; the assumption is that the center of buoyancy shifts to right the ship. The statement by dschenken describes the property of "weathervaning stability," if the center of buoyancy is above the center of gravity then the ship will be driven upright from any attitude (except exactly upside down and unperturbed.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
CHeers for that Fred.
as you've given so much help on second moments, would you put me out of my misery and tell me what I'm not doing to get second moment correct? I've broadly tried to follow the rational from the other threads in adding second moments together but this situation is slightly different..
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The "neutral axis of this structure is where? You need the second moment about the neutral axis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Thanks again. I believe the neutral axis on the waterplane (transversely) is 20m from either axis i.e. in the middle of the two sets of columns. This is what I tried to do above. However, I am not sure of the approach as I wanted to calculate a second moment for 4 columns then correct this transversely by adding the second moment of the second set of columns about the 'neutral axis'. I am not sure how to calculate the 4 columns in isolation as the longitudinal separation is not give.
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If each of the circles is 20 meters from the neutral axis (transverse) then

will put them together. If you need the longitudinal, then each distance is different, and you're right--you don't have that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Yep that is sort of what I was doing with combining 4 columns together using the logic from the other thread we had and I get the same answer.
So I now think I have an accurate second moment and underwater volume and value for KB. However, I am quite far off the model answer.
Any thoughts?
A
PS desired answer for KG is 14.49m as per the question.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What if A_waterplane is the area bounded by the structure (40m x 80 m) = 3200 m instead of 8 x 28.27 = 226 m ?
Does your answer get better or worse?
(I believe your second moment calculation is now correct.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think worse...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How are you computing BMT?

Assuming the center of buoyancy is T/2 isn't right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Transverse second moment of area about the waterplane / underwater volume.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think T/2 is only valid for simple shapes such as a wall sided ship. I can believe ~8m is correct as the majority of underwater volume is in the underwater pontoons therefore B would be relatively low in comparison to T (draft).
I think I have calculated volume correctly, I think I have calculated second moment of area correctly as you say.
That does leave me with a bit of a head scratcher.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to find the metacenter. This requires you to track the center of buoyancy as the platform tilts.
You owe me!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've been looking at this a bit, and it is interesting - this document seems to explain the derivation, starting on page 19 (4 of the pdf): http://user.engineering.uiowa.edu/~me_160/lecture_notes/lec04_2012.pdf
The general form of the question is "Find X such that 'Y= Condition' is true, where Y depends on X in some way."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good Reference!!
A much more elegant way to handle this problem than mapping the metacenter:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
As always I am forever going to owe you one!
Most impressive stuff. One thing I want to get better at/ gain a better understanding of is creating graphs during the process of calculation as you demonstrate so elegantly.
I do however believe that the problem can be solved without the need for simulating heel of the platform. I believe I had gone wrong on KB which as you demonstrate can be solved by taking moments of the centre of buoyancy of the individual components of the underwater structure vs the volume of the respective components.
I therefore believe that Morrish's formula is not valid for such structures and should only be used for a traditional ship form.
I will continue to read through your simulation of heel and try to gain a better feel of it.
I do believe that the position of the metacentre can be derived by taking the second moment of the waterplane and dividing by underwater volume as I have done.
Cheers to all and especially you Fred!
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy Wibroe wrote:
I do believe that the position of the metacentre can be derived by taking the second moment of the waterplane and dividing by underwater volume as I have done.
You're right!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See please one article about this Subject and Mathcad:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is not in English?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have looked at that as translated. And I am not sure it is telling me anything I don't already know...
As I say below the issue I think I've got is calculating second moment of area for the waterplane which is complicated by this being 8 columns spaced apart from eachother...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just to add, I understand the basics of ship stability.
The math indeed should be easy by following the simple concept of KG (Centre of Gravity to Keel) being equal to (KB + BMT) - GMT.
I believe I have calculated a relatively accurate KB using Morrish's formula for KB as above.
The area I am struggling with is calculating BMT which I believe to be equal to Jt/V i.e. the transverse second moment of the waterplane divided by the underwater volume.
I believe I have calculated the underwater volume correctly, but I am struggling to calculate the transverse second moment of area for the waterplane. I believe that the transverse and longitudinal second moments for a circle are the same and I think I have calculated second moment for a single column at the waterplane i.e. a circle correctly. What I can't get my head round is calculating for all 8 columns at the waterplane. I think this is a form of parallel axis theorem, but am struggling as the areas are obviously not connected. As I say above, I looked at this by way of calculating two sets of 4 columns and calculating about the transverse centroid of the waterplane i.e. the middle of the two sets of 4 columns.
Originally I thought about calculating second moment for each set of 4 columns but the question does not give the longitudinal spacing of the columns so do not know the X value i.e. the distance between the centroid of each individual column?
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy,
can you give me please some measurement (see attachement) ?
I found something interesting about Titanics stability here: http://titanic-model.com/articles/A_Matter_of_Stability_Trim/A%20Matter%20of%20Stability%20&%20Trim.pdf
best regards, Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
those measurements are not given.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy,
When rotating a rod, in common we have to take into account the Steiner-moments.
For instance:
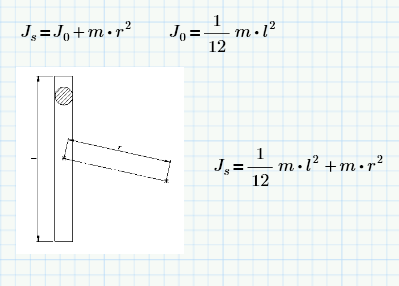
where "r" is the distance to the center of gravity of the rod.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
nnot sure I understand the application of your diagram to this problem?





