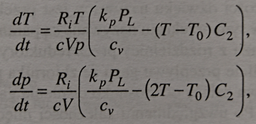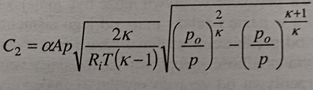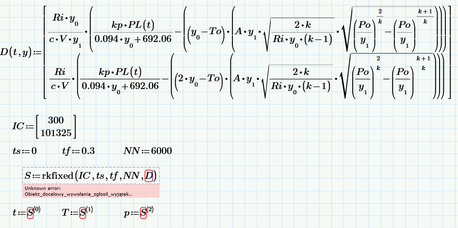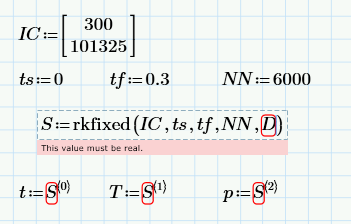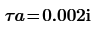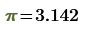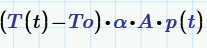Skip to main content
V
VO_103825081-Visitor
1-Visitor
August 12, 2022
Solved

System of differential equations problem

  • August 12, 2022
  • 1 reply
  • 1355 views

Hello,

 

I am trying to solve a system of differential equations to calculate the change of temperature and pressure in switchgear during an arc fault. The equations are as follows:

VO_10382508_0-1660310950136.png

where C2 equals:

VO_10382508_1-1660310984523.png

 

"T" is temperature and "p" is the pressure, PL is the power of the arc which is a function of time and is calculated earlier. The rest are constants.

I've attemped to calculate this in Mathcad Prime 8 using the rkfixed function, inputting the full equations with the C2 factored into the them:

VO_10382508_3-1660311288337.png

I've input "T" as "y0" and "p" as "y1" in the equations using the matrix index operator. The first equation if for temperature and the second for pressure. The initial conditions are for the initial temperature of 300 and pressure of 101325.

 

I'm getting an unknown error which roughly translates to "calling object expection". It does seem to dissapear when i replace one of the "y0" or "y1" variables with a constant in the second equation, but not in the first. However the results are then incorrect.

 

I would like to ask if it's even possible to solve such a system of equations using this method, or is there something else entirely I should be doing?

If it is possible, then what might be causing this error?

I'm attaching the worksheet, the shown above equations are at the botton of page 2. On page one i've calulated the currents and power "PL".

 

Thank you for any help!

 

 

Best answer by LucMeekes

This should be possible.

I'd have used Odesolve in a solve block, but rkfixed can also be used.

In an English version the error message is:

LucMeekes_0-1660313381268.png

Your function D takes the root of a difference. That difference might become negative, to result in imaginary (non-real) roots...

 

You say that "The rest are constants.", but you've replaced c.v with an expression involving T (y0)....

 

Oh, I see now that your value tau a is imaginary:

LucMeekes_0-1660314817700.png

What's this value 3.14 do in your expressions for iL1 and iL3? Shouldn't that be pi?

LucMeekes_1-1660314955732.png

Attached is my Odesolve attempt. It does produce a result.... I may have made one or more mistakes.

 

Success!
Luc

1 reply

L
LucMeekes23-Emerald IVAnswer
23-Emerald IV
August 12, 2022

This should be possible.

I'd have used Odesolve in a solve block, but rkfixed can also be used.

In an English version the error message is:

LucMeekes_0-1660313381268.png

Your function D takes the root of a difference. That difference might become negative, to result in imaginary (non-real) roots...

 

You say that "The rest are constants.", but you've replaced c.v with an expression involving T (y0)....

 

Oh, I see now that your value tau a is imaginary:

LucMeekes_0-1660314817700.png

What's this value 3.14 do in your expressions for iL1 and iL3? Shouldn't that be pi?

LucMeekes_1-1660314955732.png

Attached is my Odesolve attempt. It does produce a result.... I may have made one or more mistakes.

 

Success!
Luc

    V
    VO_103825081-VisitorAuthor
    1-Visitor
    August 12, 2022

    Indeed, sorry I forgot to mention that "cv" is a function of T and equals to 0.094*T+682.06.

    The 3.14 is meant to be an approx. of pi and for τa I just didnt think of using the determinant operator, but i got that fixed. I've also corrected some other simplifications i made earlier while calculating the currents.

     

    Your solution is working after I put the "α" constant back in the equation, since I forgot I had it removed before while I was trying to fix the error:

    VO_10382508_2-1660322012380.png

    It's meant to be a factor reducing the gas flow out the decompression flaps.

     

    I also multiplied the T(t) in the second equation by 2:

    VO_10382508_3-1660322058125.png

     

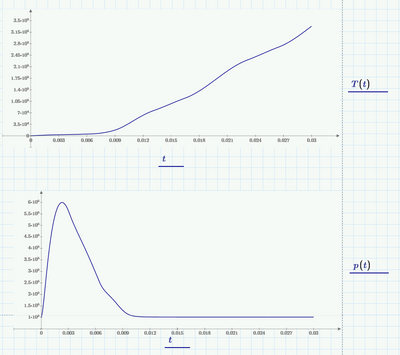
    The results are finally making some sense 🙂

    VO_10382508_4-1660322645471.png

    The "A" is the area of the pressure relief flaps and "V" is the volume of the compartment in which the arc is ignited. Changing them seems to affect the results accordingly.

    I'm attaching the worksheet where i seem to have the mistakes corrected.

     

    Thank you very much for the help!

    Terms & ConditionsCookie settingsAccessibility statement