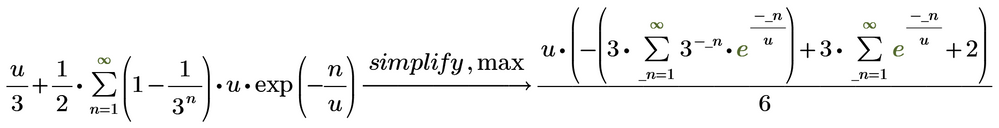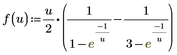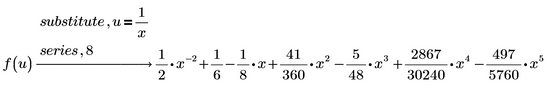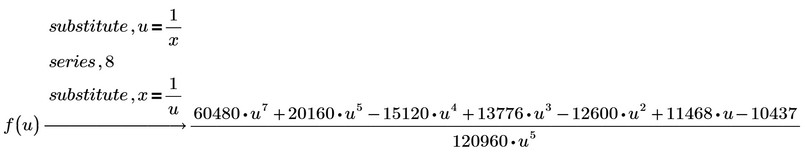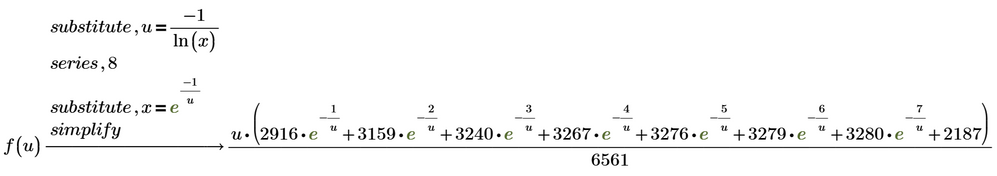Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Unable to expand an expression into a series because of a singularity.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unable to expand an expression into a series because of a singularity.
Mathcad won't allow me to expand the attached expression into a series because of a singularity. Yet the publication shows that it can be done.
Any suggestions? Please see the attachment.
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"series" expands an expression into a Taylor series. If not otherwise stated at u=0, which in your case of course must fail because of the division by zero if u=0.
A Taylor series is a (most often inifinte) polynomial, a sum of powers of u (or of u-u0). The series you want to see sure is not a polynomial and so you can't expect "series" to give you that answer.
Furthermore "series" never returns an infinite sum but only finite ones (which usually means that you get just an approximation of the initial expression).
You could tell Prime to give you a Taylor series at a position different from u=0, maybe u=1
but thats not what you would like to see.
I see no way to let Prime expand the expression to that sum shown in your pic.
You could hope that a symbolic Math program may be able to do it the other way round, simplifying the series to the initial expression, but I guess that Primes symbolic is not capable enough to do so.
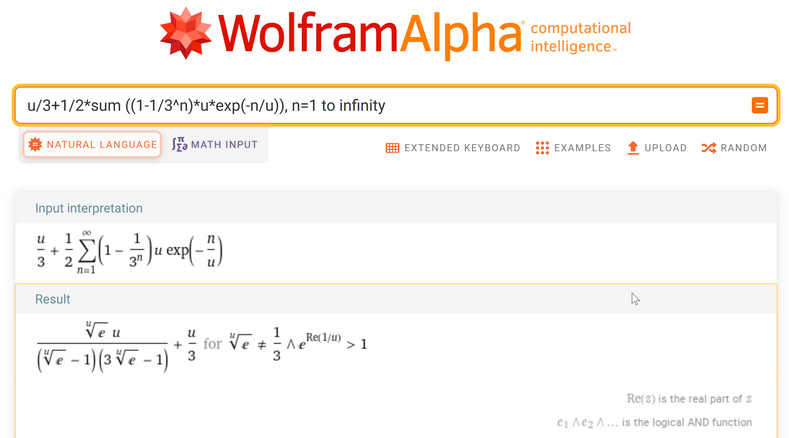
Wolfram Alpha e.g. is able to get rid of the sums and so succeeds in simplification, even though the result is not exactly the one you are starting with
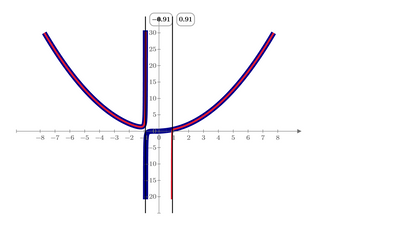
BTW, I don't think that the sum in the picture and your initial expression are equivalent for negative values of u.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Series and original equation are close 8% to 1% but not equal. For symbolics they have to be equal.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Terry and Ruby,
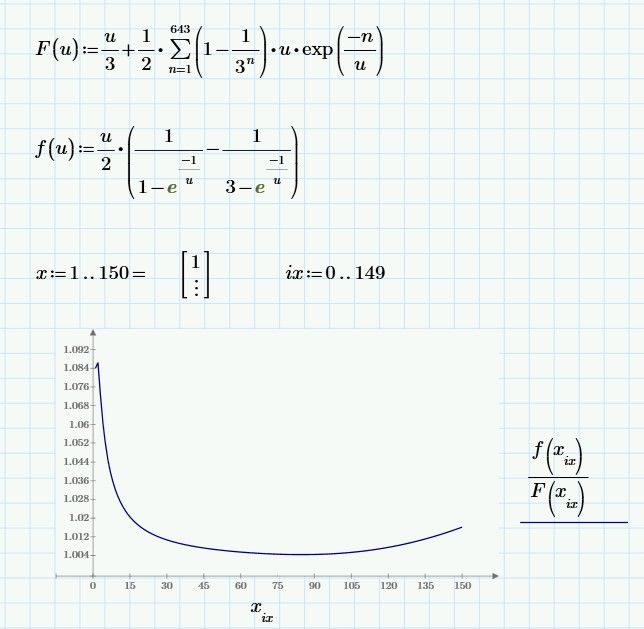
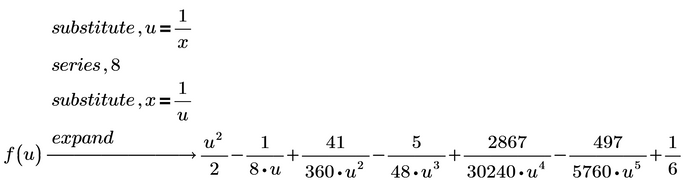
I was able to generate a single series using a substitution. However, I can't make it into a "simple summation."
Please see the attachment.
Regards,
Glen
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@gatlas wrote:
Terry and Ruby,
I was able to generate a single series using a substitution. However, I can't make it into a "simple summation."
Please see the attachment.
Regards,
Glen
With "simple summation" you mean an infinite sum, nicely displayed with the sum operator? As I already wrote in my first answer, Prime will not return that kind of display, not even for the Taylor series. It will only return a finite sum of powers, a finite polynomial. Its up to you to find out the formation law for the coefficients. Of course you can use normal calculus to do and Prime may help with the derivatives.
BTW, you may do the substitution and series in one go
and you may also follow it by the re-substitution
or
You can create completely different sums using different substitutions
or
but what for? What is the goal?
I was surprised to read that you seemed to consider the sum you achieved as being a partial success.
But this sum has nothing to do with the sum shown in the picture you posted. Its a completely different sum, even if you would be able to find its generic formula and could write it using the sum symbol.
So I wonder what the ultimate goal of your efforts should actually be?
BTW, Ruby isn't my name, its part of a silly ranking scheme here where names of stones are used. Additionally the rank expressed as a number (looks like I rank 24, whatever that may mean), and additionally we seem to have some kind of sub-ranks, at least I think thats what the "V" after "Ruby" should be. And because all of this nonsense is not enough, you also see a rank-speedometer beside the name. They could never really explain to me why this whole bunch of nonsense would be necessary.
And that's not all for the kids, there are also special icons, badges you earn, etc.
But don't let that irritate you, it's still a forum by and for adults, even if it doesn't look like it on first glance because all of this 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
https://www.glenatlasmd.com/dentistry/wp-content/uploads/2019/11/A-Tutorial-to-Approximately-Invert-the-Sumudu-Transform.final_.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I must confess that I never heard of Sumudu transform. I'll have a look at your pdf later. At a first (very short and quick) glance it looks like you need the series as an approximation for an integral - not sure, though.
But I am still confused about the fact, that you first asked for basically a series of exponential function divided by powers of 3 and then you ended up by a simple power series in 1/u. Are you just looking for any series, no matter what the summands would look like, to use it as an approximation?
I don't think that Prime would be able to get you the series you asked for or to automatically do that Sumudu transform. It just can help a little bit with the basic math, though.
One word of caution concerning the power series you found via substitution - you also have to consider the range of convergence. That power series does not represent the original function within the range |u|<=1/ln(3).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"series" expands an expression into a Taylor series. If not otherwise stated at u=0, which in your case of course must fail because of the division by zero if u=0.
A Taylor series is a (most often inifinte) polynomial, a sum of powers of u (or of u-u0). The series you want to see sure is not a polynomial and so you can't expect "series" to give you that answer.
Furthermore "series" never returns an infinite sum but only finite ones (which usually means that you get just an approximation of the initial expression).
You could tell Prime to give you a Taylor series at a position different from u=0, maybe u=1
but thats not what you would like to see.
I see no way to let Prime expand the expression to that sum shown in your pic.
You could hope that a symbolic Math program may be able to do it the other way round, simplifying the series to the initial expression, but I guess that Primes symbolic is not capable enough to do so.
Wolfram Alpha e.g. is able to get rid of the sums and so succeeds in simplification, even though the result is not exactly the one you are starting with
BTW, I don't think that the sum in the picture and your initial expression are equivalent for negative values of u.