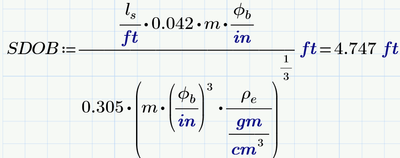Solved: Units with exponents.

wbell · ‎Dec 30, 2020

I am trying to solve an equation that has variables raised to a power (x^3) and also has roots (x^0.333). I have tried to move the dimension under the radicand, but the results still don't work.

Please see the attached worksheet and comment on what can be done for a proper solution. The answer found in Excel without any units is 4.76 feet.

Thank you for your assistance.

Werner_E · ‎Dec 31, 2020

Obviously its an empirical formula which expects the quantities in exactly the same units as you had defied them. Specifically you must use feet when defining the stemming length l.s, but centimetre when you define the density. Also the documentation seems to tell you, that the result hast to be interpreted as length in feet.

Formulas like these are not unit consistent which is disappointing and disadvantageous.

To deal with formulas like this in Mathcad, you will have to strip off the units completely by dividing each quantity by the exact unit the formula is expecting and then add the result unit at the end. That way you get the 4.76 feet you'd obviously like to see.

As Luc I suppose that the 0.333 should be 1/3 (or the third root), and so the result rather would be 4.75 feet

In this case you may also notice that phi.b can be cancelled and is not needed:

View solution in original post

ValeryOchkov · ‎Dec 31, 2020

I think you use an empirical formulf nd must use units in this formula.

One simple example:

Human_Height = Human_weight + 100

Human_Height = (Human_weight/kg + 100)*cm

LucMeekes · ‎Dec 31, 2020

The other problem is that you have some 'magic numbers' in your equation.

What is 0.042 , and what is 0.305 ? Do (should) these numbers have units?

What is the expected unit of the result for SDOB? If that is ft, then 0.042 could have unit ft^1/3 and if 0.305 would be ft, you'd get ft for SDOB, but ONLY if you express the power of the bracketed set as 1/3, instead of 0.333

Success!
Luc

Werner_E · ‎Dec 31, 2020

Obviously its an empirical formula which expects the quantities in exactly the same units as you had defied them. Specifically you must use feet when defining the stemming length l.s, but centimetre when you define the density. Also the documentation seems to tell you, that the result hast to be interpreted as length in feet.

Formulas like these are not unit consistent which is disappointing and disadvantageous.

To deal with formulas like this in Mathcad, you will have to strip off the units completely by dividing each quantity by the exact unit the formula is expecting and then add the result unit at the end. That way you get the 4.76 feet you'd obviously like to see.

As Luc I suppose that the 0.333 should be 1/3 (or the third root), and so the result rather would be 4.75 feet

In this case you may also notice that phi.b can be cancelled and is not needed: