Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Using Prime 3.0, the determinant function does not handle a matrix with complex numbers. Don't how to fix it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using Prime 3.0, the determinant function does not handle a matrix with complex numbers. Don't how to fix it.
When I load a matrix up with al reals the |A| or det(A) works fine and returns the value. If I add a +1i or any imaginary number to an element, the |A| or det(A) returnb 0. This frustrating since I have programs that use this alot for filling arrays in a linear systems problem.
Solved! Go to Solution.
- Labels:
-
Other
- Tags:
- determinant_solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
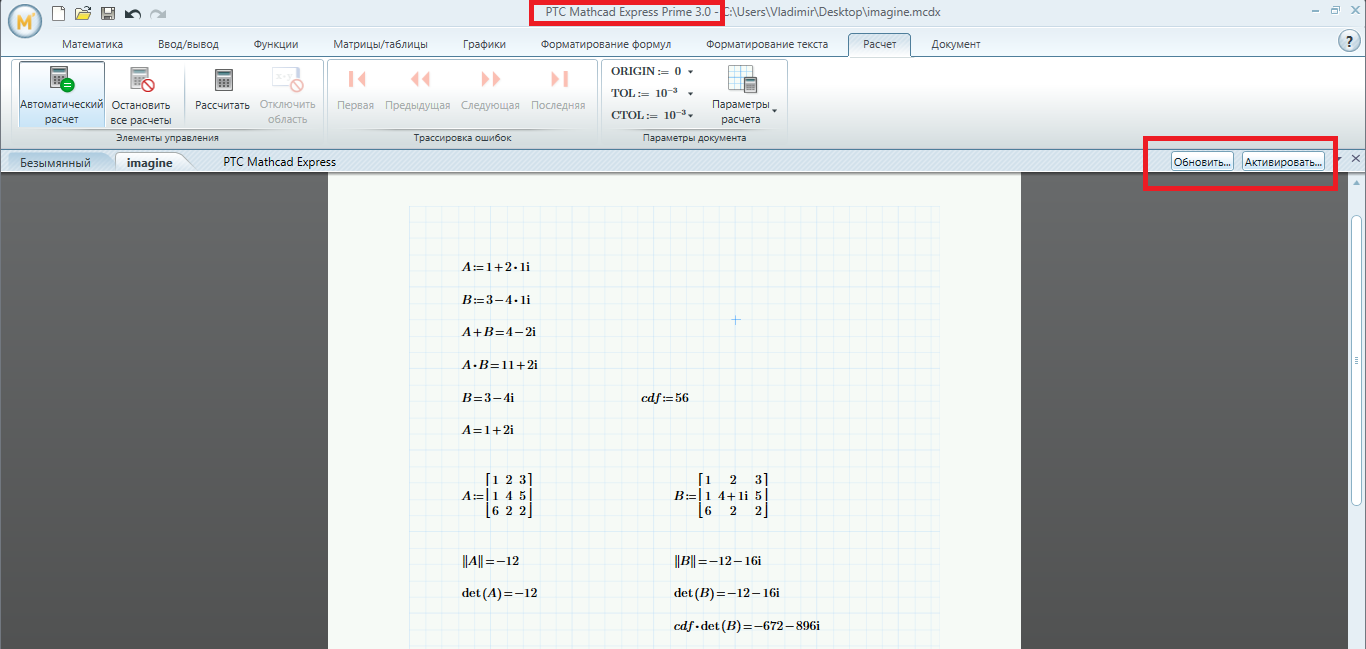
See my answer above and attach your file with this bug to the message.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Foster, Fred, Luc,
From what source did you get your Mathcad Prime Express version?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
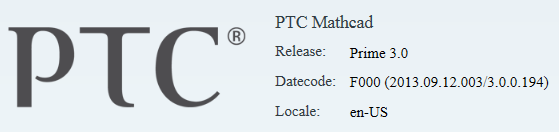
I do not have Express, full up Prime 3.0:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
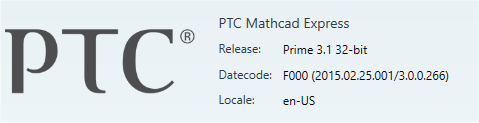
I use Prime 3.1 32-bit (F000 (2015.02.25.001/3.0.0.266)) with .NET Framework 4.6.1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fresh install. downloaded from PTC website
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for this information - we're currently looking into this issue.It would help our investigation to know what versions of Prime on what versions of .NET seem to be exhibiting the problem. For those of you who see this determinant issue, can you let us know the following:
- The version of Prime you are running (Prime 3.0, Prime 3.1)
- The bitness of the version of Prime you are running (32 bit, 64 bit)
- The operating system you're running on
- The bitness of your operating system
- The version of .NET you are running - details on how to do that can be found here: https://msdn.microsoft.com/en-us/library/hh925568(v=vs.110).aspx
Even though Prime 3.0 is certified to run on .NET 4.0 and Prime 3.1 certified on .NET 4.5.1 and .NET 4.5.2, if you are running those versions of Prime on unsupported versions of .NET that information will still be useful to know.
Many thanks,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy,
Sorry I had to forward your questions to one of our IT consultants that's been helping. In either case nothing is fixed at this point. I don;t know if you have a list of contacts here at Ethicon, but his name is Mike Craycraft. I'll forward his responses.
It is Mathcad Prime 3.0 and I am pretty sure it's 64 bit.
Thanks,
Foster
x3112
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear All:
Thank you for all the support and suggestions. After Andy's response we check the Net version and had to make the change. That fixed it. So I'm finally back up and running Prime 3.0 and can get back to my job.
Thanks again,
Foster
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a Prime function to interrogate the exact Prime version and bitness of the application?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
If you click on the Mathcad button in the top left of the application you will see the app menu. Select 'Options' and in the 'About' tab in the dialog that appears you'll find the product 'Release' information (Prime version and bitness).
Many thanks,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK Here goes:

So the above is for:
I have access to another PC. When I transferred the source (.mcdx) file to it and ran it, it displyed the same (remembered) values, but when I pressed the recalc button, it just crashed!
So I retyped the important part:

And this is for:
Good luck!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't forget send your issue to tech support by using "Mathcad Support Center" (you can do it, even if you use Express version of Mathcad Prime): Mathcad Support Center
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
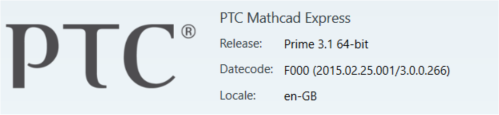
Windows 10 64-bit (1607, 14393.693)
PTC Mathcad Express Prime 3.1 64-bit, F000 (2015.02.25.001/3.0.0.266)
.net 4.6.2 (DWORD version 394802)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All - thank you for the information you've provided in this thread, once again it's been extremely helpful for the Mathcad team. We've found and fixed the observed determinant issue in Prime 4.0, releasing on March 6th next week. Though you may find the issue resolved if you roll back your version of .NET to the version supported by the version of Prime you are running (.NET 4.0 for Prime 3.0, .NET 4.5.1 or 4.5.2 for Prime 3.1), the nature of the issue means that we can't guarantee another Microsoft update now or in the future won't reveal it again. The recommended way to resolve this is therefore to upgrade to Prime 4.0.
Many thanks,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy,
And whether there was a beta testing of this 4th version of the program (is there will be an invitation for users for a beta of testing of future releases of Mathcad Prime too)? How the situation (and date of release) with an next service release of Mathcad 15 M050 is?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"the nature of the issue means that we can't guarantee another Microsoft update now or in the future won't reveal it again. The recommended way to resolve this is therefore to upgrade to Prime 4.0."
To prevent this bug in the future, wouldn't it be better that PTC offers a free upgrade to Prime 4.0 for all users that have bought any version of Prime ![]() .
.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So much for fixing this bug in Prime 4.0:
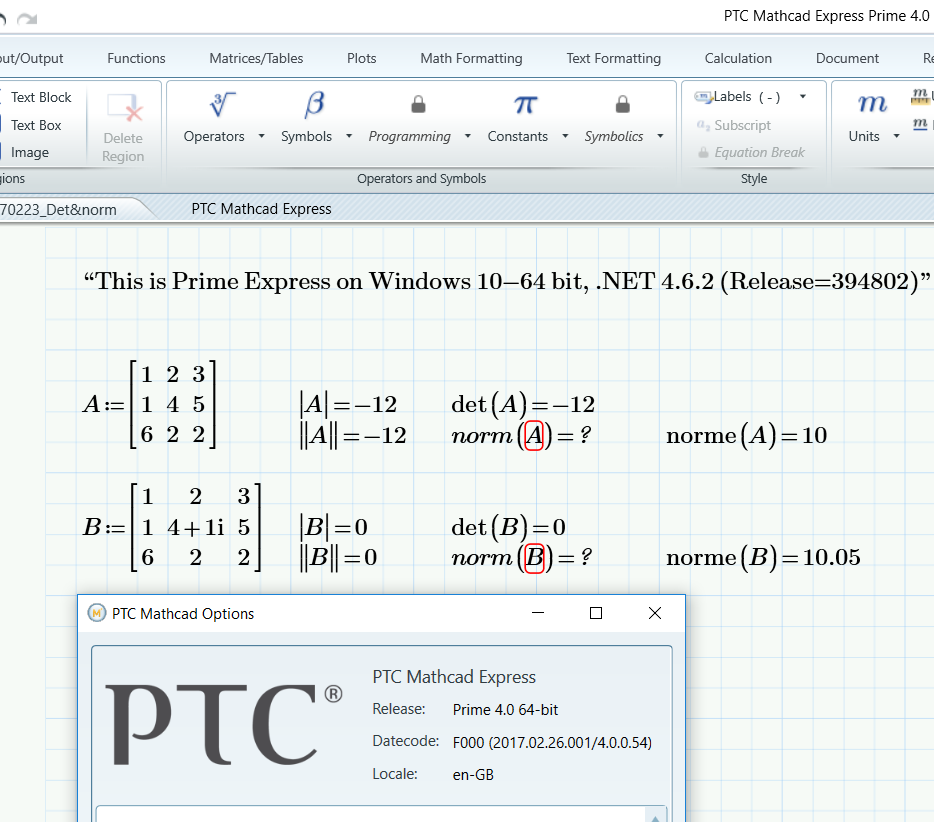
![]()
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc - apologies! The issue that is fixed in Prime 4.0 is the determinant issue. The determinant of a complex matrix does return the correct result in Prime 4.0.
The behavior you see is due to a difference between how the norm() function and the norm operator work. The norm() function, as defined in Help, only returns the norm of vector v. Because there is more than one matrix norm, the norm operator returns the determinant of a square matrix and the norm of a vector (I notice we have an issue in how that is documented that I'll get cleared up for Prime 5.0).This behavior is a topic of discussion here and it may be something we look at moving forward based on input from users such as you.
Many tanks,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
![]()
I always thought that |B| and det(B) were supposed to return the determinant of matrix B (if it is a matrix, and it is square).
Did you see that both |B| and det(B) return 0 instead of the supposed -12-16i, which is exactly in line with what the OP was complaining about?
Please correct me if I'm wrong.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc - I do not see that here. Could this be as simple as needing to calculate the worksheet when you open it in Prime 4.0 Express? We don't recalculate on open (to preserve results from the last save) so if that was the first time you opened the worksheet in Prime 4.0 Express you'd see the results from the previous save (in your previous version of Prime). If you haven't already, can you try recalculating? We tried that here - creating your worksheet in Prime 3.1 on an unsupported version of .NET so we saw the issue and then saving and opening that worksheet in Prime 4.0 Express. On open it looked like your screenshot but on recalculate we see this:
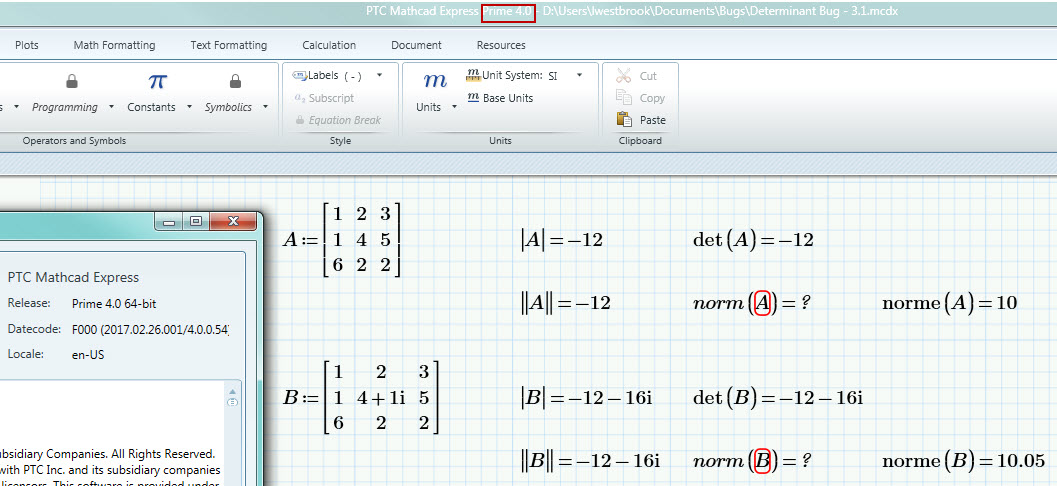
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andrew,
My apologies.![]() You're right, I forgot to recalculate.
You're right, I forgot to recalculate.
Having Prime remember the last results is sometimes a blessing
(if you're limited to Express and open a sheet with symbolic results)
and other times it's not
(if you forget to recalculate)
Regards,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution of this "problem" is quite simple. You should perform calculations of determinant symbolically. This is strange because you can multiple or invert matrices with complex elements numerically. This not the first and not the last strange behaviour of Prime.
Robert
- « Previous
-
- 1
- 2
- Next »





