Valery's Travelling Salesman Problem

[AlanStevens]

Apologies for starting a new thread, but I couldn't see how to upload a Mathcad file near Valery's video.

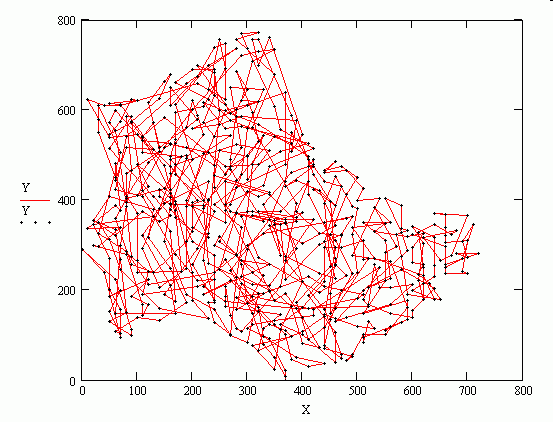
The attached file is rather simplistic and very inefficient, but it would be interesting to see how it compares with Valery's method. There is plenty of scope for improving the efficiency, including, possibly, incorporating a Metropolis-style algorithm (in which there is a small probability of accepting a worsening rather than an improvement from time to time).

I've saved the file in M11 format, but I've not tested it in M11.

Alan

Note: I've edited this - the current attachment calculates the total distance correctly, which the original didn't!

Also made it somewhat faster.

[jeanGiraud]

Thanks Alan,

It computes in reasonable time [5 ... 10 mn ?] Mathcad 11.

Steven Finch [Mathsoft] had a work sheet,,, in lost worlds !

Jean

[jeanGiraud]

The traveling salesman was included in Mathcad numerical recipes pack [version 5 /6 ?]. Still advertised to Mathsoft but it ends to a "girls zooooooo"

[ValeryOchkov]

>The traveling salesman was included in Mathcad numerical recipes pack

Yes - see the function anneal here

[jeanGiraud]

Thanks Valery for the hint,

Do you have the Mathcad program "anneal(,,,)" ?

Jean

[ValeryOchkov]

I am searching myself, sorry!

[ValeryOchkov]

Thanks, Alan, for the interest on my task!

Bur sorry - the optimal tour in Luxemburg is here http://www.tsp.gatech.edu/world/lutour.html

[AlanStevens]

"...Bur sorry - the optimal tour in Luxemburg is here http://www.tsp.gatech.edu/world/lutour.html"

Yes! I've increased the speed of the program considerably from the one I posted earlier, but the best it finds in a reasonable time is a distance of about 25000 as against the actual best of 11000+. Clearly the logic would need to be modified (completely altered!) to improve further. I don't intend to take it any further myself, there are lots of programs out there that do this (mainly Matlab and Maple it seems; not Mathcad unfortunately!). It was an interesting Sunday afternoon excercise though!

Alan

[ValeryOchkov]

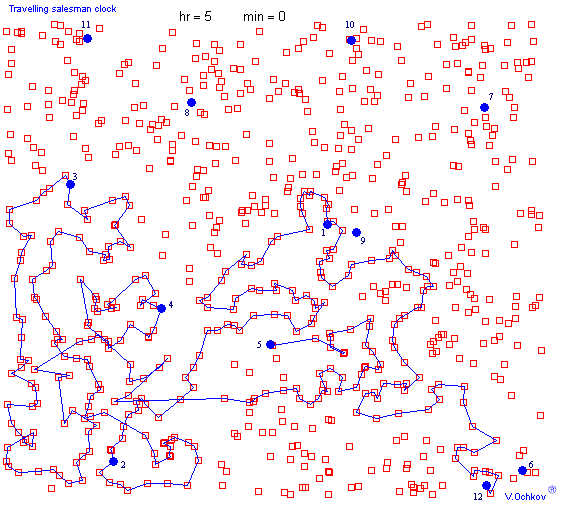
My hobby (beiside Mathcad of couse) is unordinary clocks and watchs.

An unordinary clock for the land of clocks & travelers (Switzerland) - see the video in attach!

[ValeryOchkov]

>but it would be interesting to see how it compares with Valery's method

No problem - see the attach!