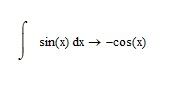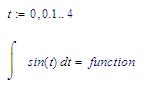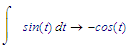Velocity function will not integrate

[remslie]

Hi,

I am trying to simulate a base excitation using a velocity versus time waveform as the base excitation. I have imported an excel file and developed a velocity time function using "linterp". When I try to integrate this it flags an error.

Further down the sheet I use an indefinite integral to derive the base input displacement from my velocity waveform. Is this OK. Any assistance would be appreciated. Cheers Ross

[LucMeekes]

Your GY(t) is defined for only numerical applications. Asking for the indefinite integral (the integral without borders) is a symbolic operation. You can't even numerically evaluate an indefinite integral for symbolically known functions like sin(x):

in contrast to:

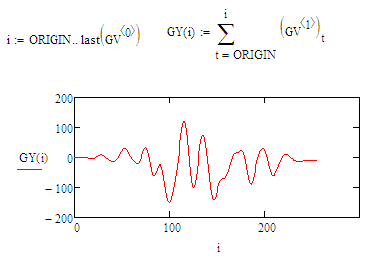
To determine the integral of the dataset that you input, simply summing is the best way.

Your datapoints are discrete values. You cannot achieve more accuracy by interpolation.

So:

Success!

Luc

[remslie]

Luc,

Many thanks for your interest, knowledge  and feedback on my integration issue.

Cheers

Ross

[AlanStevens · Accepted solution]

1. In M15 the indefinite integral of sin(x) works ok!

2.  I've fixed some errors in the sheet and pointed out some mistakes in units - see attached.

[LucMeekes]

"In M15 the indefinite integral of sin(x) works ok!"

Yes, symbolically, but try that numerically...

Luc

[AlanStevens]

@ Luc

"Yes, symbolically, but try that numerically..."

Of course not numerically!  As you demonstrated, the result is a function, not a number (though I missed the fact that you'd shown a numerical = rather than a symbolic -> !).

[remslie]

Alan,

Thanks again for coming to the rescue!. My text in the sheet said the input waveform was acceleration when in fact it should have read velocity. This means that your integrated waveform is in fact displacement. I rejigged the equations to reflect this and bingo I have a solution. Brilliant!😁

Cheers Ross