Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Volumes of Revolution - Hyperbola
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volumes of Revolution - Hyperbola
Hi,
I'm hoping someone can help me with a question about volumes of revolution of hyperbolas.
I have a question asking for the volume of a hyperbola shape (see attached ppt).
I understand that I need to re-aarrange in terms of (x^2) and intergrate etc.
But I want to know what limits i apply to find the definite integral and what i use the dimensions for.
Thanks in advance
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First you have to know/state what kind of surface of revolution you have to calculate the volume for (hyperboloid of one or of two sheets). The formula you gave assumes revolution around the x-axis. Where are the axis in your drawing? Given the usual arrangements of axis this would mean a hyperboloid of two sheets but then it would be absolutely unclear which volume should be calculated as the drawing is not symmetrical with respect to the horizontal x-axis.
You can't calculate anything as long the goal is not clearly specified and as long as the drawing and its dimensioning does not fit the equation given. Either one of the two is either wrong or approximated in such a manner that it can't be told what dimension we should rely on - diameters (x-values) or heights (y-values).
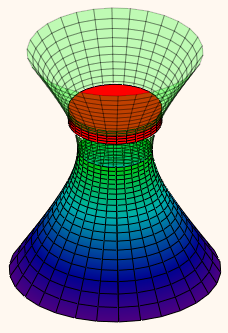
I guess that you are supposed to calculate the volume of a hyperboloid of one sheet like in the plot below. As of the axis we assume y-axis going up, x-axis to the right and z to the front. You slice your volume in a lot (infinite number) of tiny, cylindrical slices like the red one in the plot below. The radius of the red cylinder is (using the aforementioned convention) x, the height is an infinite small y-difference dy. So the volume of a single red slice is x^2*pi*dy. Now you have to sum up (integrate) all those slices from y=ybottom to y=ytop and we get for the volume V=pi*int(x^2)dy from ybottom to ytop.
To calculate it you mus express x^2 in terms of y, which is pretty easy with the given equation.
To get the limits you will have to dissolve the conflict drawing dimensioning versus equation given.
EDIT: As the insertion of a pic in the text seems not to work again, I make it an attachment
To give you an idea about the difference you get using either the dimensioning or the given equation:
1) If we assume that the values for A,B,C,D and E are correct, we get a slighty different equation (564.06 instead of 560 and 3582.67 instead of 3600) and the volume is 322944,86 m^3
2) If we assume the given equation is correct and also the values for A and E, we would get different values for B,C and D and the volume is 325346.89 m^3.
Thats a difference of approx. 2400 m^3!
A third way to interprete the given sheet would be to assume that the equation, the sum C+D and either A OR E are correct, but I couldn't be bothered to try these variants, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You still have a questing pending, I guess. http://communities.ptc.com/message/233220#233220
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like you confused a lot of things:
The drawing suggests a rotation along the vertical y-axis (hyperboloid of one sheet) while what you did in your MC sheet looks like a revolution amongst the horicontal abscissa (hyperboloid of two sheets). In any case you are missing the constant pi and are using the wrong variable of integration - its either int(x^2, dy) or int(y^2,dx).
Even worse, the equation given does not match the values in your drawing. E.g. if I take the diameters A, B and E as given, with the equation given you would get D=85.16m (not 89.5) and C=19.98m (not 24.5).
You might want to sort things out first and also look up the correct formula for the volume of revolution.
If you first consider how to do the calculations manually, it would be easier to help doing it using Mathcad as a tool. A better drawing including axis might also help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's actually an assessment question so the values in the poorly drawn diagram are given to me.
Am I correct in making to following assumptions then;
1) to begin you re-arrange in terms of x or y.
2) use the formula for volumes of revolution (was on the second page but I obviously never saved it before attaching), being Pi* int(y^2)dx.
3) the values for the upper and lower limits are what I'm strugging to understand. How do I determine these?
Its kind of a question for both using mathcad as a tool to solve but also to understnad how to actually solve these questions!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First you have to know/state what kind of surface of revolution you have to calculate the volume for (hyperboloid of one or of two sheets). The formula you gave assumes revolution around the x-axis. Where are the axis in your drawing? Given the usual arrangements of axis this would mean a hyperboloid of two sheets but then it would be absolutely unclear which volume should be calculated as the drawing is not symmetrical with respect to the horizontal x-axis.
You can't calculate anything as long the goal is not clearly specified and as long as the drawing and its dimensioning does not fit the equation given. Either one of the two is either wrong or approximated in such a manner that it can't be told what dimension we should rely on - diameters (x-values) or heights (y-values).
I guess that you are supposed to calculate the volume of a hyperboloid of one sheet like in the plot below. As of the axis we assume y-axis going up, x-axis to the right and z to the front. You slice your volume in a lot (infinite number) of tiny, cylindrical slices like the red one in the plot below. The radius of the red cylinder is (using the aforementioned convention) x, the height is an infinite small y-difference dy. So the volume of a single red slice is x^2*pi*dy. Now you have to sum up (integrate) all those slices from y=ybottom to y=ytop and we get for the volume V=pi*int(x^2)dy from ybottom to ytop.
To calculate it you mus express x^2 in terms of y, which is pretty easy with the given equation.
To get the limits you will have to dissolve the conflict drawing dimensioning versus equation given.

EDIT: As the insertion of a pic in the text seems not to work again, I make it an attachment
To give you an idea about the difference you get using either the dimensioning or the given equation:
1) If we assume that the values for A,B,C,D and E are correct, we get a slighty different equation (564.06 instead of 560 and 3582.67 instead of 3600) and the volume is 322944,86 m^3
2) If we assume the given equation is correct and also the values for A and E, we would get different values for B,C and D and the volume is 325346.89 m^3.
Thats a difference of approx. 2400 m^3!
A third way to interprete the given sheet would be to assume that the equation, the sum C+D and either A OR E are correct, but I couldn't be bothered to try these variants, too.





