Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Weibull fitting problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Weibull fitting problem
Can anybody point me to my error. I can't get a decent fit for my data; see attached MC15 file.
Thanks in advance
Raiko
P.S. For some reason the website does not accept the MC15 file claiming that "...the contents of the attachement doesn't match its file type." henec, I've added a pdf.
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure about the Gaussian.
Here is a direct comparison side by side (worksheet attached):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The data aren't distributed according to the Weibull distribution that you have traced in your graph (for s<=1). So you will never be able to adapt them to Weibull's distribution. The sample is small. How do you say it is distributed according to Weibull? With a larger sample it may turn out to be Gaussian.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
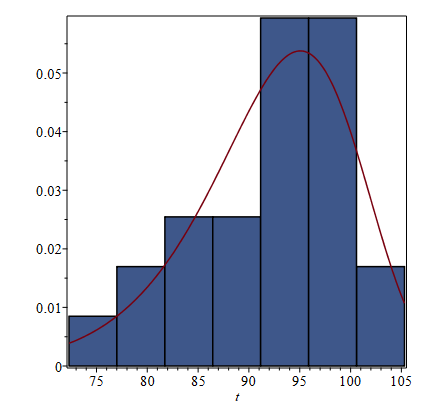
Maybe a scaling problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
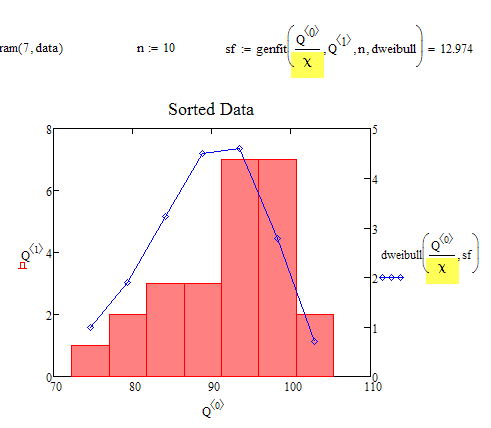
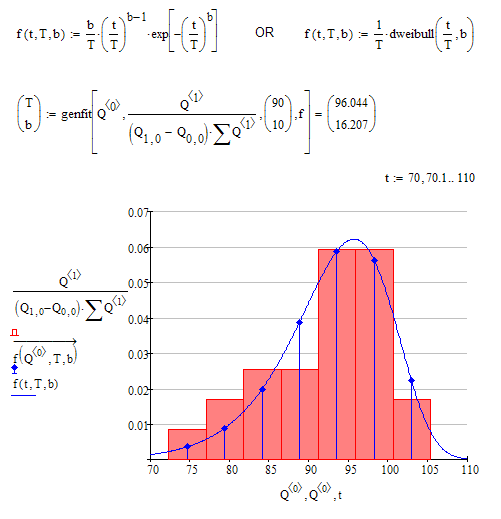
Mathcads weibull unfortunately is standardized to scale parameter (in German: charakteristische Lebensdauer) T=1.
To fit we need a function with two parameters, scale T and shape b.
Guess thats the way to achieve that in Mathcad:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F M is (I believe) correct, This should be a normal fit; if you're measuring hardness that's what I'd expect. You can get a normal fit as shown--the same basic method as Werner did for the Weibull.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure about the Gaussian.
Here is a direct comparison side by side (worksheet attached):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
sorry for the late reply but I wasn't in office for a few days. Thanks a lot to all of you guys for your effort and thank you Werner for the solution.
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
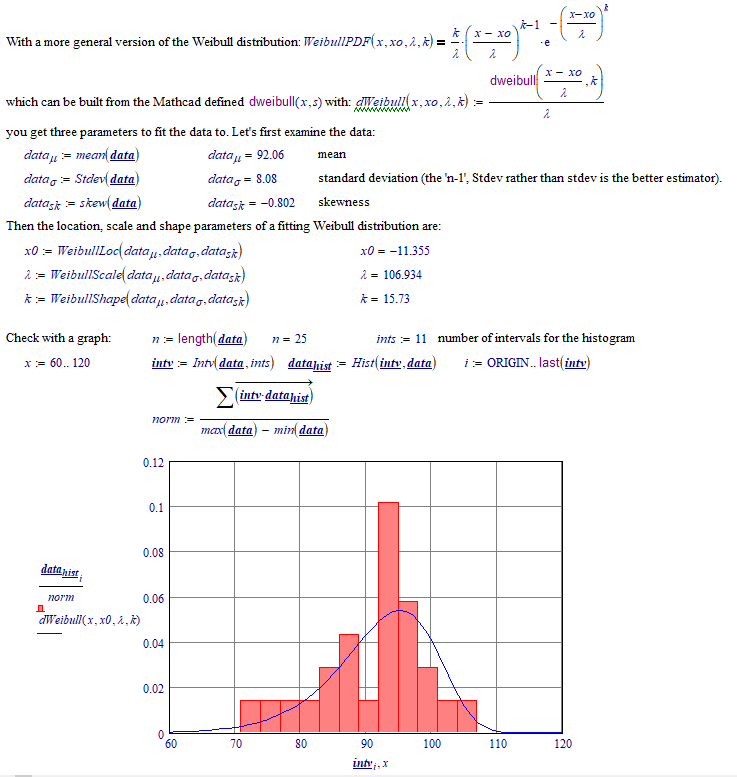
Your data is skewed, hence a Weibull distribution is more plausible than a normal distribution.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure that I agree.
Using the probability plotting of the Data Analysis Extension for both Normal and Weibull:
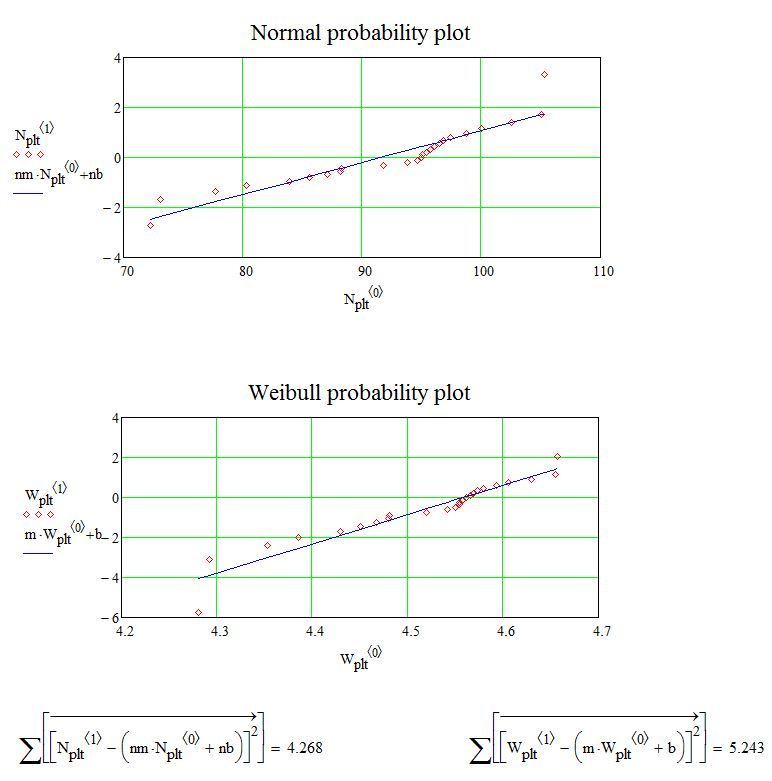
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is no realistic way to know what the distribution should be, and 25 data points is surely not going to allow you to determine it statistically (although I have not done any statistical calculations to prove that ![]() ). Maybe there is some systematic error that skews the hardness measurements, maybe not. If not, it's probably Gaussian. If there is such an error, it probably does not follow any statistical distribution. So what distribution to use in the fit likely depends on the end goal more than anything else.
). Maybe there is some systematic error that skews the hardness measurements, maybe not. If not, it's probably Gaussian. If there is such an error, it probably does not follow any statistical distribution. So what distribution to use in the fit likely depends on the end goal more than anything else.