Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
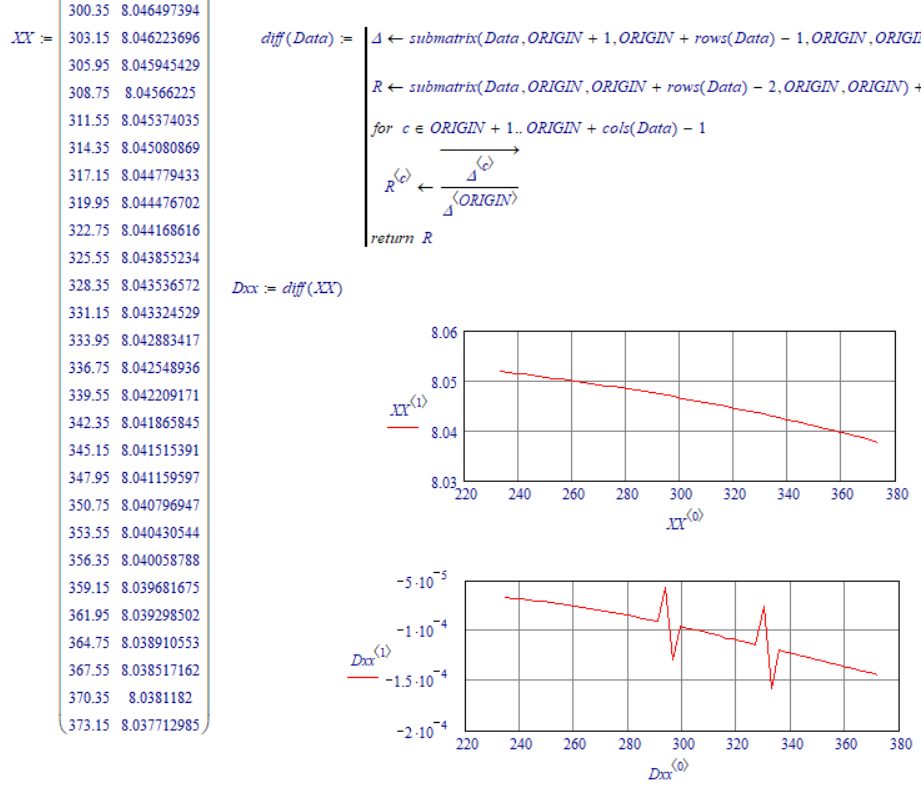
data set differentiation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
data set differentiation
Hello,
I'm trying to take the first and second derivative of my data set (frequency vs temperature). I've used the standard method to define a function via cspline- interpolation and take the derivatives. However, from the attached worksheet, it is seen that the plot of the derivatives have peculiar behavior and I'm afraid the result may not be reliable.
Could anyone make a suggestion on this issue, please?
Thank you in advance,
Payman
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
-
Programming
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks to me like a simple quadratic fits pretty well - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can't see all of your sheet. This is what I get with brute force differentiation:
I wonder if it would be better to approximate the curve with a mathematical expression (part of a parabola?) and then do the differentiation on that model...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Luc.
Do you know why the cspline routine produces the spikes on the first derivative? I tried also with a higher number of data points and get the same issue.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As far as I know (regarding splines not much) spline routines just try to find a curve that nicely passes through all your data points. If you have a couple of 'funny' points, they will be included in the curve (Note that DJF's graphs appear to show these funny points!). So I guess there's no difference when you use spline curves or the raw data to calculate a derivative.
Modelling the behaviour with a mathematical function (as Alan reportedly did) will get rid of any funny points.
Maybe it's worth-wile to investigate how the funny points got in: was it the oven switching in or out?. If you remeasure the curve, do you get spikes at the same temperatures?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
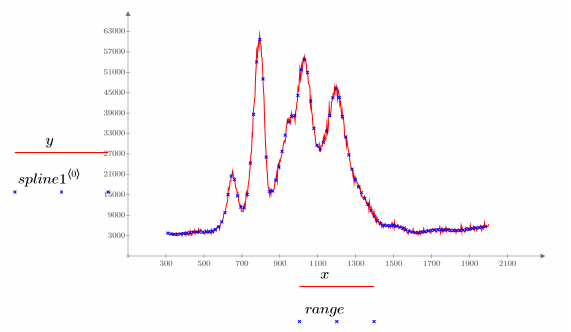
It goes without saying that it's up to the engineer or scientist to understand their data. Test data is usually full of noise so a mathematical fit is often the appropriate solution to make working with the data easy (or possible). Of course, those blips may actually mean something. I've just found the b-spline functions very powerful provided you understand what you're doing.
The ptc example shows a good plot of data I'd hate to work with without a b-spline.
https://help.ptc.com/mathcad/en/#page/PTC_Mathcad_Help%2Fexample_least_square_spline.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All of the spline fits develop piecewise solutions: a series of functions (in the case of cspline cubic equations) that pass precisely thru each data point. The result is a cuve that looks like a great fit.
If you have real-world data there will be small errors in each data point. (Where the actual value may be 4.374862, it gets recorded as 4.375.) In these cases the enforced precision of Mathcad forces the cspline curve thru 4.375. The spline fit forces the point and the first derivative at the point, but the second derivative is unconstrained.
If, for the reported data, you have a theoretical curve shape (perhaps from the physics of the experiment) a better way is to do a least-squares fit of the data. regress does a least-squares fit to a polynomial, so all derivatives of the curve will remain smooth.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A little clarification - Fred is correct in the c,l&p splines and linear interpolation will pass through the points. Others do not - such as b-spline, bezier, polynomial, or localized polynomial. Different tools for different jobs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@payman wrote:
Thank you, Luc.
Do you know why the cspline routine produces the spikes on the first derivative? I tried also with a higher number of data points and get the same issue.
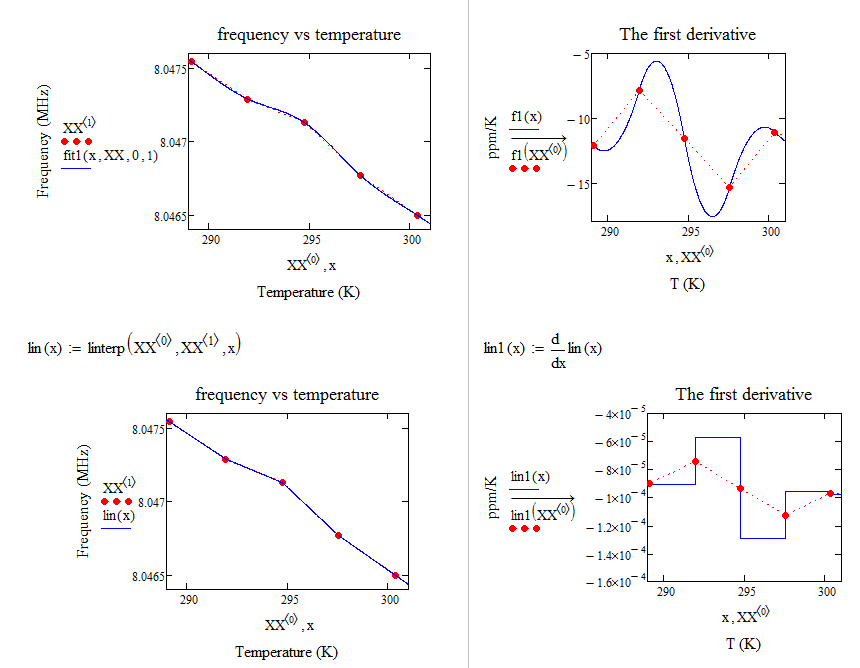
Maybe it helps if you zoom in at those "funny points" to understand what happens or to look at the effect a simple linear interpolation has.
While in your case a quadratic fit seems appropriate, another option might be to use one of the data smoothing functions Mathcad offers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks to me like a simple quadratic fits pretty well - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Alan.
Using the regress routine produces smooth results in both the first and second derivatives. It looks more reliable than cspline routine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator