Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
definite integral bug
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
definite integral bug
I work with WIN7, WIN XP, and WIN 2k. I use MCD-15, -11, -2001.
In all cases I find an error when calculating a definite integral. The error looks as follows: the location of a constant "a" inside the integral leads to a different solution compared with the case with the consant "a" outside the integral. This behaviour hurts the basic mathematical relationship in (1):

The result of a simple calculation approach can be studied in the following graph (solid = wrong = left side of (1)n; dotted = right = right side of (1):
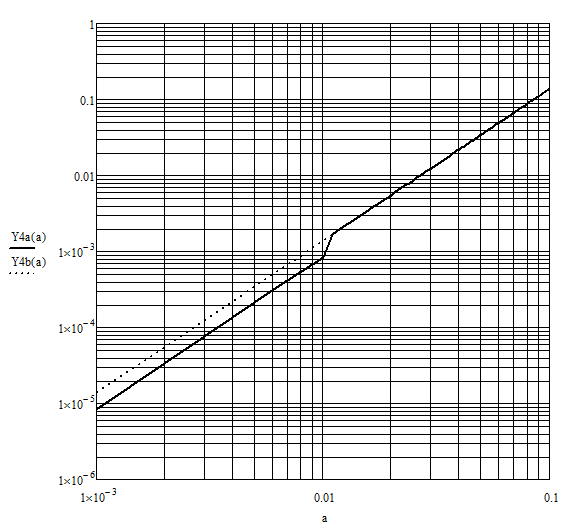
In most cases it won't be possible to move constants outside the integral, hence, there should be a bug correction asap!
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am too lazy to retype whyt you had done, but have you tried changing TOL and CTOL?
I guess what you experience are just normal round off errors but I may be wrong.
For numbers stored in a computer, usually neither the commutative law applies nor the distributive. If this is the case her its not a Mathcad specific problem.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
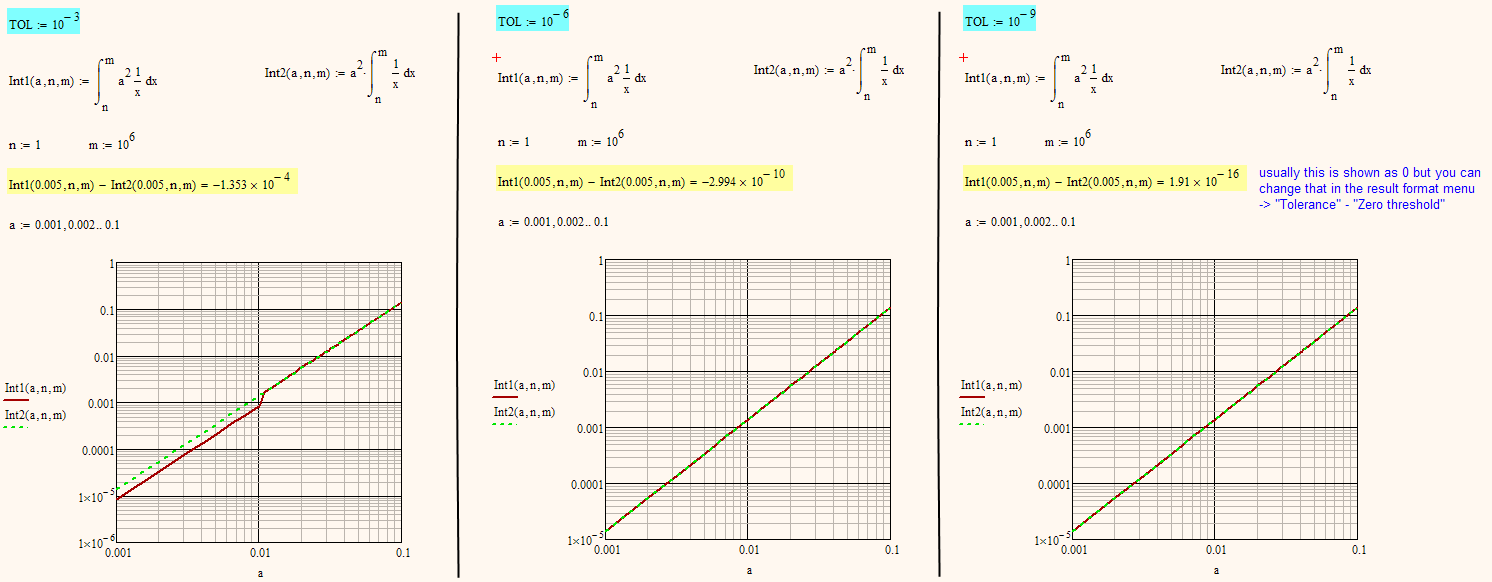
I am less lazy today, and - voila! Seems you did not try changing the tolerance value.
You must always keep in mind, that you are doing numeric calculations using finitely many computer numbers with limited accuracy.
Here is an example which shows that summation is not commutative using this set of numbers:

Your example shows, that the distributive law is not validi in the set of computer numbers.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for your extensive remarks. I’ve expected something like this. I know TOL’s influence.
However, I didn’t assume that Mathcad makes the precision of the integral’s result at the left side of (1) additionally dependent on the size of the constant “a”, and not only dependent on f(x), n, m, and TOL. At the right side of (1) there is no additional dependency on “a”.
I see, insofar, Mathcad treats both sides of (1) differently.
Usually, the precision of a result can be expressed in the number of digits after the decimal point. This is not the case here. A high precision of eg three digits after the decimal point is not a precision per se. It can only be achieved with the right TOL setting, which becomes in most parts of my work several magnitudes smaller (up to 10e-10) than the default TOL setting. The latter case leads to a lower precision with three digits after the decimal point.
That’s why it seems to me that the shown circumstances are not (or not enough comprehensibly) reflected in the explanations about TOL and its application.
I understand why Mathcad includes this kind of solution mechanism for integrals. Additionally, Mathcad shows many warning tips. Ergo – a satisfying answer to the following question(s) could delete my bug feeling:
Based on the number of digits after the decimal point and to gain the highest result quality possible why isn’t there a built-in warning with a tip for a better TOL value setting?
Or:
Why isn’t there a built-in automatic-TOL-value-setting possibility that ensures best result quality, fully dependent only on a selected number of digits after the decimal point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Why isn’t there a built-in automatic-TOL-value-setting possibility that ensures best result quality,
Thats something you sure have to ask the devlopers of MC (good luck in doing so;-)
But lower values of TOL do not always mean more accurate results (thats the nature of some of the numeric algorithms implemented) and so Mathcad can't automatically detect, which numeric result is more accurate. Furthermore you'll often run into problems when setting TOL and/or CTOL too low and may run into the "calcuation does not converge" error message.
If you need more accurate results than a numeric approximation algorithm (numeric integral) is able to provide, you'll have to resort to symbolic calculations but then Mathcad sure is not first choice and even with more specialized software you are limited - not every problem can be solved symbolically.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are intrinsic limitations to the precision of numeric computing. In the case of Mathcad that's about 14 to 15 decimal places (double precision floating point numbers). However, that's not the issue here. Numeric integrals are solved iteratively, which is to say it starts with an approximation and then successively refines that approximation until it's "good enough". The question then arises, 'what is good "enough"'? In Mathcad the stopping point of built-in iterative calculations is defined by one of the built-in constants TOL or CTOL. The default value for both is 10^-3. If you set them to smaller values iterative calculations will take longer to converge, and it's possible they may not converge at all.
Could the current behavior be improved? Yes. I have a long standing gripe that TOL and CTOL are absolute, rather than relative, which means they don't depend on the magnitude of the number being evaluated. Fixing this would not be that difficult, but doing so would likely break a lot of existing worksheets (all of which could be easily fixed, but breaking existing worksheets is never a good thing), so I doubt it will ever happen. In your example, the kernal of the integral is being scaled by about 10^-6 to 10^-2 when a is included, and that is the problem. If TOL were relative rather than absolute you would not see this problem (or perhaps more accurately, you would either see it for all values of a, or none of them).





