Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
e^x - (e^x*1i)^-1i - (e^pi)*sin( x + [pi/2] ) and symbolic solve fully ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
e^x - (e^x*1i)^-1i - (e^pi)*sin( x + [pi/2] ) and symbolic solve fully ?
Hello Everyone.
e^x - (e^x*1i)^-1i - (e^pi)*sin( x + [pi/2] ) and symbolic solve fully ?
Thanks in advance for your time and help.
Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
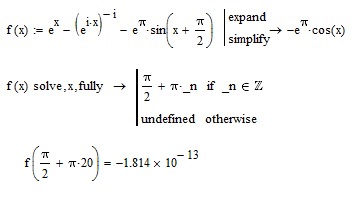
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, F.M. ![]()
![]()
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
^(-beta).jpg)
Open video with windows media player.
The video shows that, in the first graph, by increasing the angle θ of the point z at each turn around the origin, the function of z, in the second graph, remains on the same branch. There isn't the jump on a new branch. Then the origin is not a critical branch point aand the function is single valued.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, F.M. . I think my question is not clear, (sorry) :
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Loi Le,

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, F.M.
I greatly appreciate your time and help. ![]()
![]()
![]() They are very, very helpful to me.
They are very, very helpful to me.
Best Regards.
Loi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Loi Le,
I would solve the problem as follows:

Greetings
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have lost track of which problem should be solved, but Mupads simplification

is wrong! Those two expressions are not equivalent.
Sometimes Mupad even has a slight idea of this problem and refuses further simplifications (see below) but ever so often it simplifies too simple and wrong, or lets say, incomplete, as it chooses arbitrary one specific value out of an infinite number of possibilities, ignoring all the others.
Here is a situation where MuPad at least is somewhat cautious:#

and from a mathematical point of view we have to consider that
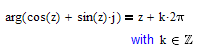
even though "arg" is often limited to a certain range (like 0..2pi or -pi .. pi) for convenience reasons (to make it a unique function, like we do with arcsin, or the square root in the real domain). But in complex calculations of expressions we have to consider the many multiples of 2pi.
So we get

and therefore
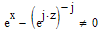
Zero is just one of an infinite number of possible outcomes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
I consider the results I obtained accurate. Moreover, mathcad, for me, is not in error.
Bye
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To say, that the solution of x^2=4 is x=2 is also accurate and not in error. nevertheless its incomplete - thats my point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I disagree.
1) Its not a function at all because its not unique valued.
2) Hope you agree that e^(j*z)=e^(j*(z+k 2pi))=e^(j*z)*e^(j k 2 pi)
And now (....)^(-j)
Its similar to z^(1/2)=...2 values or 1?
Its a question of definition of exponentiation which is different in R and C.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad's results are no proof for anything.
That was the point all the time! Mathcad does not respect the multitude of possible result but only chooses one.
The representation of a complex number with Real- and Imaginary part is unique, but the representation with magnitude and phase is not, unless you arbitrary limit the phase (to -pi to pi or to 0 to 2pi). Thats the reason for the multi-valueness of exponentiated expressions.
We have a similar case with the third root (or any other), which as you probably know, has three results in C.
Mathcad will only give you the so called "main value" (and this makes sense in many situations, even if we are missing the two other results)

This often is confusing for people as they would at least expect -2 as result. But the main value is defined as the one with the smallest phase.
Thats the reason we have

in Mathcad as sort of a compromise. But thats another story.
Mathcad will only present you all three results if you rewrite it as an equation
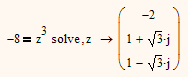
Nevertheless the same three results are valid for (-8)^(1/3) but Mathcad is not showing all of them.
We have a similar situation here:

I am sure why Mathcad does not simplify the constraint to

and I doubt that its a necessary constraint.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
.png)
Best Regards
Loi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
assume, x = real
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It follows my attempt to solve this equation:
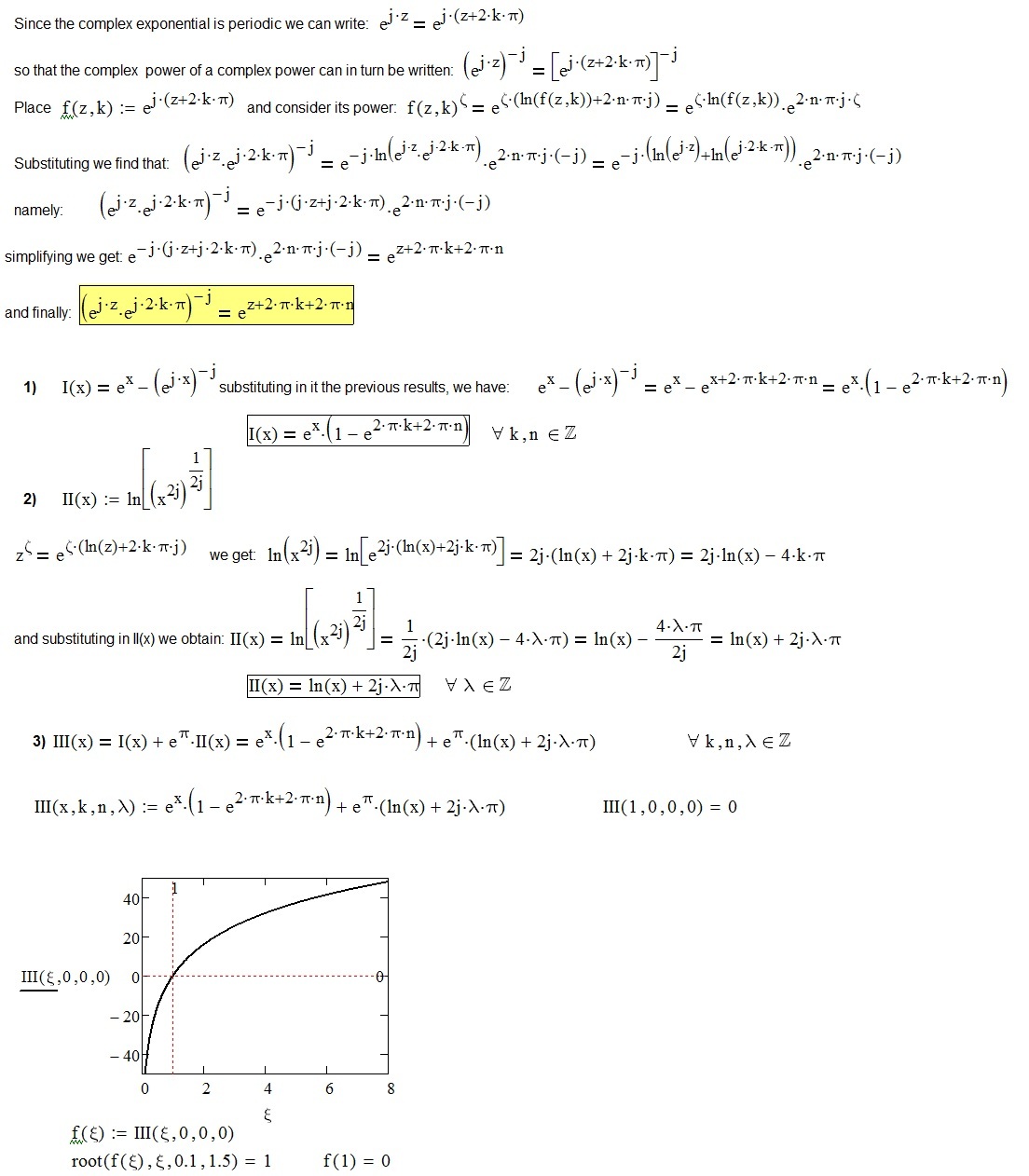
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Four days ago you wrote here:

and now you write
![]()
Bravo! I guess now finally you got it that this expression has more than one single "result"! At least here on earth - I'm not sure about heaven 😉
But there is no need to distinguish between k and n here. You may simplify 2 pi k + 2 pi n to just k'*2pi with k' in Z.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
....Offenbar Wunder geschehen im Himmel und auf der Erde!
Doch alles hat eine logische und matematische Erklärung.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
assume, x = real
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
assume, x = real
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
assume, x = real
Regards.





