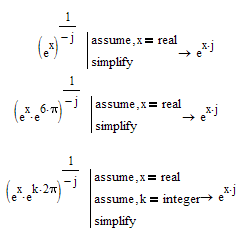Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
e^x = [e^(x*1i)]^-1i ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
e^x = [e^(x*1i)]^-1i ?
Hello Everyone.
The question : e^x = [e^(x*1i)]^-1i ?
Thanks in advance.
Best Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it is. Here's why:

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Luc. ![]()
![]()
I guess we have both : = and ~= . and I am missing some things if I say :
Best Regards.
Loi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
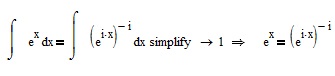
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I also agree with both of you, F.M. and Luc.
Best Regards.
Loi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
....Ok.... however my solution is formally, the most simple and elegant ....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I think I don't understand the following simple solutions :
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
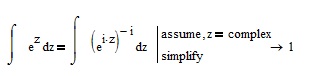
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But this does not proof that the two integrands are fully identical, given that one of them is not single valued!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
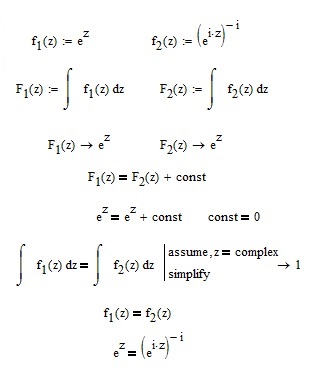
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As explained below: don't trust Mathcad when it comes to more complex (pun intended) pure mathematics. Mathcad is not a mathematical proofing tool. When Mathcad/Mupad applies a function or a functional operator on an ambiguous expression or function, it applies it just to one instance (which it chooses at will) and thats the reason your integral yields e^z in both cases. Thats also the reason for why the symbolics and the numerics sometimes yield different results - they chose different instances of the same multi-valued expression. The reosn most of the times is that the symbolics first simplifies and then chooses, while the numeric immediately chooses an instance.
And then you might want to lookup how integration is defined in C and what to do, when the integrand is not a unique, unambiguous function!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner for the clarification, I will always keep them in mind.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Exponentiation in the complex domain is not so easy and straightforward as in the real domain.
Mathcad, as already often stated, is not really good in that cases. Simply because Mathcad tells us that a specific equation has just one solution sure is no proof that thats true and simply because Mathcad tells us that two indefinite integrals are equal does not proof that one of the integrands might not be a multivalued expression.
For problems like yours its better to use mathematics and not Mathcad.
But even though Mathcad has its limits here, there seems to be a reason why Mathcad does (correctly) NOT simplify to 1 here:
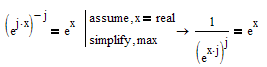
Or please notice the difference here:

The reason seems to be that if x is a complex number, then (e^x)^j is multivalued, while e^(x*j) is not.
So it looks like MuPad's developers were aware of the difference concerning exponentiation in R and in C and so are quite careful in some simplifications. This is often annoying when we implicitly assume the real domain but MuPad insists that if not told otherwise the domain is set of complex numbers (this was easier at the times of Maple).
And while they were aware of the problems with exponentiation, they had not fully implemented the correct math (or Mathcad is not using the full potential of Mupad, not sure).
The truth is that for real values of x

So its a multi-value expression.
And even Mathcad can at least help making that plausible: