- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
how to use controls to switch inputs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
how to use controls to switch inputs
hi,
i'm sure this is an easy question for a lot of you. i don't understand the help or built in examples for this topic. i have a variable i want to switch using some type of control. i can't figure out how to do it. i got the slider switch working, which is nice. but the other controls i can't figure out. i attached the matchad 15 worksheet. not interested in a prime solution, if there is one.
there are five choices for the variable z. i have just been manually typing in the choices. if you could show how this would work for as many of the controls as possible, i would appreciate it. it's something i'd like to learn how to do.
thanks
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the attached file you find two ways for the selection of "z".
The first one uses the text box from the Web Controls. They are easy to use, won't trigger the popup window when you open the sheet (because Web Controls don't allow for scripting) but are rather inflexible. You have to manually hardcode the names you want to see in the list box and also the values they should return. I had chosen to return values from 0 to 4 which then are used as an index in a nested vector consisting of your choices.
The second approach uses a scripted textbox and i modified one found in the collection of RichardJ. It uses two input lists (one with the names to be displayed and one with the values z should take).
If you are interested in scripted components, you sure should have a look at Richards collection here: https://community.ptc.com/t5/PTC-Mathcad/Extra-Components-and-Controls/m-p/450450
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the attached file you find two ways for the selection of "z".
The first one uses the text box from the Web Controls. They are easy to use, won't trigger the popup window when you open the sheet (because Web Controls don't allow for scripting) but are rather inflexible. You have to manually hardcode the names you want to see in the list box and also the values they should return. I had chosen to return values from 0 to 4 which then are used as an index in a nested vector consisting of your choices.
The second approach uses a scripted textbox and i modified one found in the collection of RichardJ. It uses two input lists (one with the names to be displayed and one with the values z should take).
If you are interested in scripted components, you sure should have a look at Richards collection here: https://community.ptc.com/t5/PTC-Mathcad/Extra-Components-and-Controls/m-p/450450
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks werner,
the web control is nice. i switched the slider to a list, using your example. i never would have figured that out. thanks a lot.
anthony
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
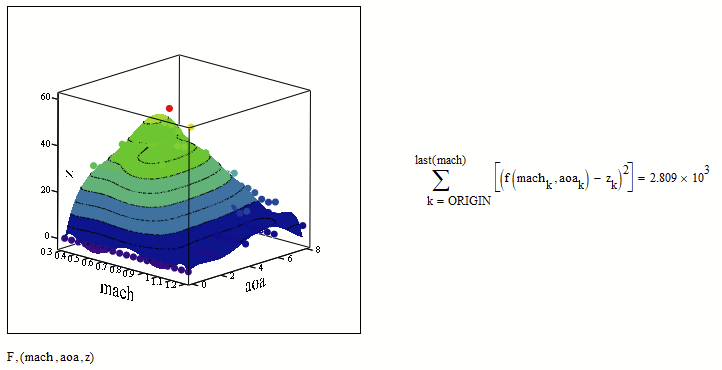
i attached an update with more of the quick sheet info i used for the analysis. i can tell visually that a different approach, that i have been using, is better. however, i have a dumb math question, for the approach in the mathcad file. with 2d spreadsheet curve fits, there is the r^2 value you can use to mathematically judge the fit. with the 3d poly curve fits, is there an equivalent? i didn't see anything in the help. i imagine there must be something, but it doesn't seem to be mentioned in the help files. the hidden area has the math, which i stole from the help quick sheet. i have the web control from werner in there as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure if that is what you are looking for, but wouldn't calculating the squared sum of errors (or the square root of that value) do the job?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks, that should work good.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may consider using the MSE (mean squared error) which would mean that you divide the sum given above by rows(mach).
That number would not depend on the number of data points given.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i did a google search after your first reply, to see if that would work. one link was to the current mathcad help. it seems they deprecated the stuff from the mathcad 15 help (which i used). so there may be a better way to go about this. the current help seems to have built in error output. but it's all too complex for me to understand. what i have now is sufficient to give me what i was looking for. so this is just a learning exercise for me.
i asked two questions in one thread. it seems like i could only say one thing was the answer. however, you provided two correct answers. so sorry about that.
this is an interesting topic for me. i was impressed with mathcad's plotting. it's fairly easy to do what i wanted. however, i have multiple data sets. i noticed that it seems to ignore the extra data. so that is why the plots and curve fits are looking weird. i think i would have to average the extra data and then import that. but it doesn't seem worth the trouble given the 3d curve fit isn't going to work. i'm using multiple 2d curve fits and that works good enough for what i need. it looks like the curve fits for aoa vs performance are smooth 2d polynomials. however, the change with mach has a lot of abrupt shifts. unfortunately, the 3d poly fit just blows through it and can't seem to pick it up well.
PS; the biggest problem with the 3d fit is that you can't enforce boundary conditions. the cl and cm data are zero at zero aoa. but the 3d fit is all wavy and crazy. so there are just a lot of problems with this approach. but that is what i wanted to find out. i wanted to make sure there wasn't a better way than what i was already doing. so it let me see that as it is now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Higher order polynomials tend to be wavy. You can try to fit a different type of function manually (mabe using a solve block with minerr) or you may consider using an interpolation (linear or one of the three cubic spline types) instead of a fit/regression.
But you would have to provide the data in a different way.
1) you would have to go rid of the extra data. For example for mach=0.85 and aoa=2 you provide two different values for lod, 16.784 and 61.111.
2) The data should be provided by two vectors, an 19-element vector for mach (values 0.3, 0.35, ....1.2) and a 5-element vector for aoa (values 0,2,4,6,8). The data for lod should be provided in a 19 x 5 vector.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
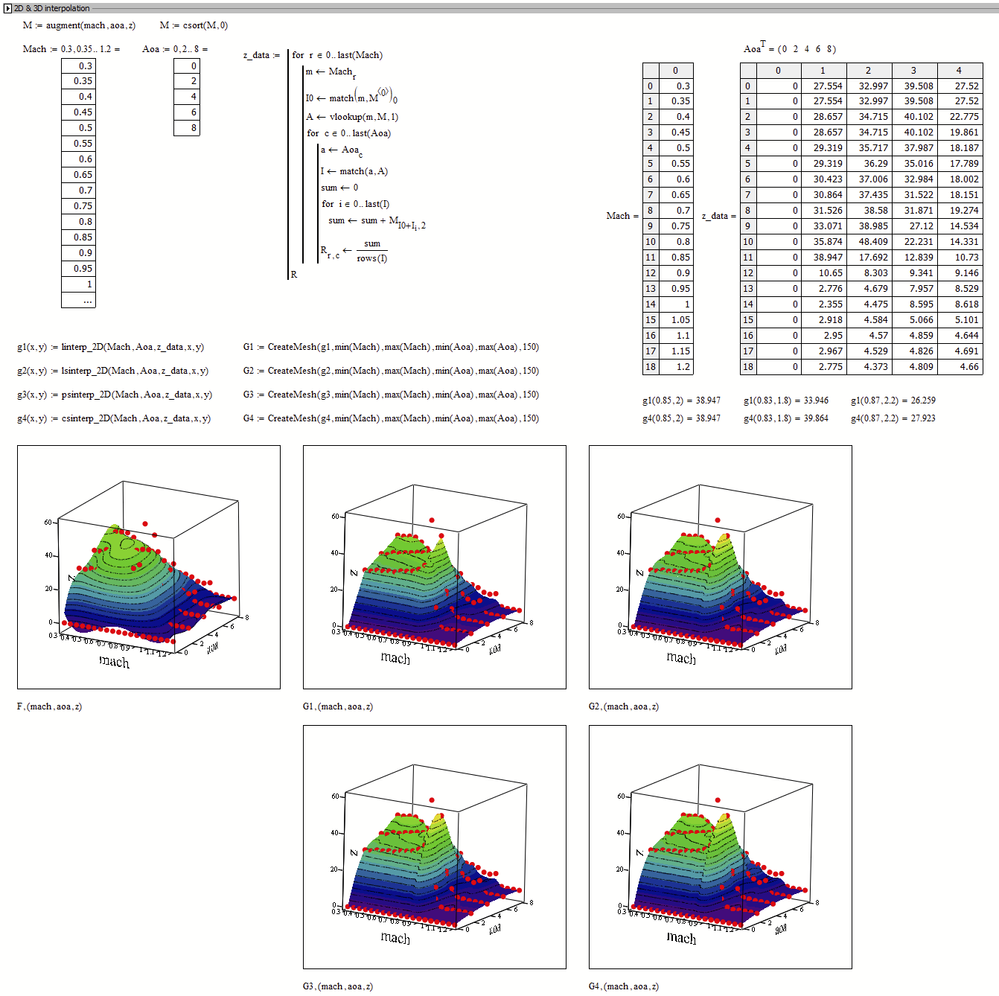
Here are examples of the interpolations I was talking about. Its just a quick hack. The vectors Mach and Aoa are hardcoded but of course their values should be derived from the data provided.
If or more data points are directly on top of each other (as in the example mentioned above) all are simply averaged. That is the reason why not all points lie on the surface in the graphic.
The interpolation routines are in the collapsed region above. The built in multi-dimension cubic spline interpolations could only do it if Mach and Aoa would be of the same dimension, so I could not use it.
As you can see, the difference between the linear interpolation and especially the three cubic spline interpolations is not too big. In general, csinterp_2D tends most to oscillate, but never as violently as a higher-grade polynomial regression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks again. i was wanting to look into linear interpolation but couldn't figure out how to do it. this is very helpful. yeah the data is weird in spots. there were two different tests done and sometimes they don't agree. when i first brought in the data, i was hoping mathcad would use 'all' the data to find the best fit. but it looked like it was having problems plotting it. i'm not sure what it was doing for the actual fit.
this data is ultimately for use in Fortran codes. I have curve fit it in 2d using LibreOffice Calc. I call the fits based on the Mach number. It's working pretty good. I thought about using linear interpolation or a combination of 2d curve fits and linear interpolation. It seems to work good enough without the linear interpolation. The other option was some sort of formula f(x,y) = z. But it looks like the polynomials wouldn't be good. So it was helpful just to see that in Mathcad.
i've never tried to do anything like this in Mathcad. I couldn't have done it without the built in quick sheet and your help. it's a good learning experience for me. i think there are better ways, based on the new Mathcad help. but without examples close enough to what I'm trying to do, it's hard to figure out. I'll study what you sent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried adding linear interpolation to the Fortran codes and it helped. So I'll be using that going forward. I attached an update of the Mathcad file. It has the base data that the codes use. The data uses 2d polynomials for AoA vs. performance. Then a bunch of those curves for a wide range of Mach numbers. Lastly, I linear interpolate between the Mach numbers. So many of the plots in the Mathcad file should represent the base data.
The Mathcad file is useful to show that trying to fit a 3d polynomial to the data doesn't work.
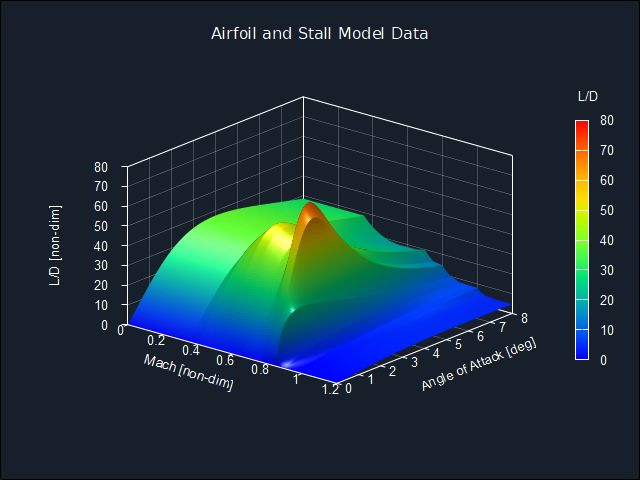
I made a separate Fortran code that plots all the data in gnuplot. With that code, I can increase the x and y steps, to get a high level of resolution to the plots. Here is a high-res gnuplot of the L/D ratio.