Hi everyone,
I am programming a Newmark's Method that involves 3 masses. During the process I need to fill a matrix that represents how the stiffness vary along time, and well at that point I have a problem. I don't really know how Mathcad solves de flow of the iteration, I mean, I don't know if I can ask it to do an operation with a previously calculated value, but I need to do it.
The error is "this value must be a scalar" all the variables involved in that "if" are scalars so I don't know why it's not working.
I really appreciate your help. Thanks in advance.
PS: Excuse me for my poor english, I'm Spanish.
ACCEPTED SOLUTION
Accepted Solutions
Similar answer as in the previous thread:
Lets begin with the error message:
You can use previously calculated values in a program, but ...You compare a difference of x with y.2c. x is a vector whose elements are three element vectors, so x[i-x[i-1 is a vector while y.2c is a scalar. Thats throwing the error. Whats the purpose of that comparison? Would you like the absolute value of the difference of those vectors to be smaller than the y values?
The break statement can never trigger as you are asking if a three element vector (x[i) is equal to a scalar (R). Again it does no harm but could be deleted. Don't know what the purpose of that break should have been, but you have be aware that it will only break out of the j-loop.
The statements to the left of your four if statements should be instructions to be executed if the condition to the right of the if is true. In your program these are boolean expressions themselves. Think they should be local assignments.
I think that there is an error in condition of the four if-statements. The first compares the difference of x[i and x[i+1 while the next three would compare the diff between x[i and x[j.
Strongly think that this should be the same for all four. If you use j you run into troubles as j is runníng from 1 to 3 and at the beginning 2 and three are invalid indices for x. If i+1 is meant, then the j-loop would be useless and should be omitted. The same calculations are done three times which doesn't make sense. Does no harm but slows down without benefit
See attached. This time I haven't deleted the j-loop and the break statement.
BTW, if I am right concerning the 4 if statements you could delete the four of them and replace them with a single line (see below).
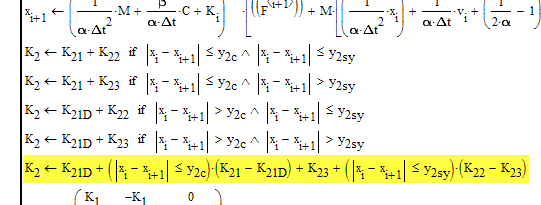
Edited: While the one-liner above is correct its not so easy to read and comprehend. Have it replaced by two if/otherwise statements.
Maikel Nite wrote:
PS: Excuse me for my poor english, I'm Spanish.
I can only wish that my Spanish was as good as your English.
Similar answer as in the previous thread:
Lets begin with the error message:
You can use previously calculated values in a program, but ...You compare a difference of x with y.2c. x is a vector whose elements are three element vectors, so x[i-x[i-1 is a vector while y.2c is a scalar. Thats throwing the error. Whats the purpose of that comparison? Would you like the absolute value of the difference of those vectors to be smaller than the y values?
The break statement can never trigger as you are asking if a three element vector (x[i) is equal to a scalar (R). Again it does no harm but could be deleted. Don't know what the purpose of that break should have been, but you have be aware that it will only break out of the j-loop.
The statements to the left of your four if statements should be instructions to be executed if the condition to the right of the if is true. In your program these are boolean expressions themselves. Think they should be local assignments.
I think that there is an error in condition of the four if-statements. The first compares the difference of x[i and x[i+1 while the next three would compare the diff between x[i and x[j.
Strongly think that this should be the same for all four. If you use j you run into troubles as j is runníng from 1 to 3 and at the beginning 2 and three are invalid indices for x. If i+1 is meant, then the j-loop would be useless and should be omitted. The same calculations are done three times which doesn't make sense. Does no harm but slows down without benefit
See attached. This time I haven't deleted the j-loop and the break statement.
BTW, if I am right concerning the 4 if statements you could delete the four of them and replace them with a single line (see below).
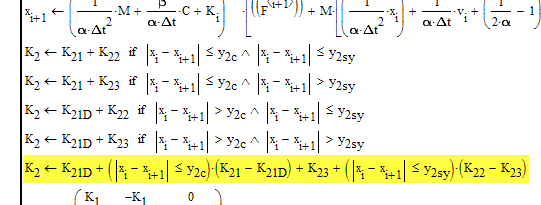
Edited: While the one-liner above is correct its not so easy to read and comprehend. Have it replaced by two if/otherwise statements.
Really really useful these answers.
In particular I'm really amazed with your answer Werner.
I'm checking the programme, and now I have more clear a couple of things, I've understood why it wasn't working the xi-xi+1 operation. It's because I really wanted to do the operation that its showed in the picture that I've attached, I wanted to pick up the second component of the x vector and substract it from the first one in each iteration and compare the result with the y2c. To do so I've tried to traspose the vector and do the diference.
While it is outside the program it works as I want but when it is inside, Mathcad says that the value must be a scalar. Any clues?
PS. I know that I've said before, but I really appreciate your help
While it is outside the program it works as I want but when it is inside, Mathcad says that the value must be a scalar. Any clues?
It works inside as well as outside and thats the reason it has to fail. Did you notice the paranthesis around the -1? These mean that its a 1x1 matrix, not a scalar. You used the column selector to get that value from the transposed vector. That selector will give back a 1-column matrix (vector) in every case, even if the content would only be a single number.
But what you want is far easier to achieve.
x is a vector consisting of a number of 3x1 vectors.
So first you select one of those inner vetcors as you did with x[i.
Then you want to select the first and second element of that inner vector and subtract. So again you will use the matrix index: (x[i)[0 - (x[i)[1
Using spacebar correct Mathcad would even make the parenthesis for you.
If you want to stick to the transpose, you would have to type ((x[i)^T)[0,0 - ((x[i)^T)[0,1 
As I understood the three elements in each vector x[i represent the distance of three masses. Why do only the first two contribute to the matrix K? And why is it the difference of those two - I thought these three are independent from each other.
What about the break line and the j-loop? The first will never trigger and the loop is unnecessary (so far at least).
A laste one: is it necessary to keep all those matrices K for every step of iteration? If no, you could replace K[i and K[i+1 (and K[0 above) simlpy by K and save some memory.
