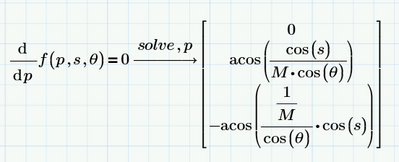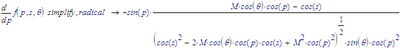Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
mathcad prime 6 cannot solve an equation correctly
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
mathcad prime 6 cannot solve an equation correctly
Hi everyone,
I'm trying to use Mathcad prime 6 to solve a symbolic equation, but I cannot get the exactly same results as what I got from mathcad 15.
I don't know why the prime 6 cannot solve this symbolic equation, but mathcad 15 could.
Anyone know the reason or some hints, please let me know.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Welcome to the forum.
A picture paints a thousand words..... A worksheet helps much more.
So: you should ALWAYS attach your worksheet.
Other than that: Fricas (the new symbolic engine in Prime 6) may be less capable in solving 4th order equations than MuPad. Switch symbolic engine to the 'classic' symbolic engine and see what happens.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
attached are the two files I mentioned. One is using mathcad 15, the other one is using prime 6.
The symbolic equation is exactly same in the two files, but prime 6 cannot give me the solution of one of them.
If possible, please help me take a look at the files, thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually I tried to switch the calculation engine to "Legacy symbolic engine", but still doesn't work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was afraid of this: you have to check the labels of the variables you use.
In the laste expression in Prime, there are two different p's, the p as an argument to f() is labelled as a 'variable',
the other two p's (the one next to d, and the p to solve for) are labelled 'automatic' shown as (-).
make sure they are all labelled the same, and it should work.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
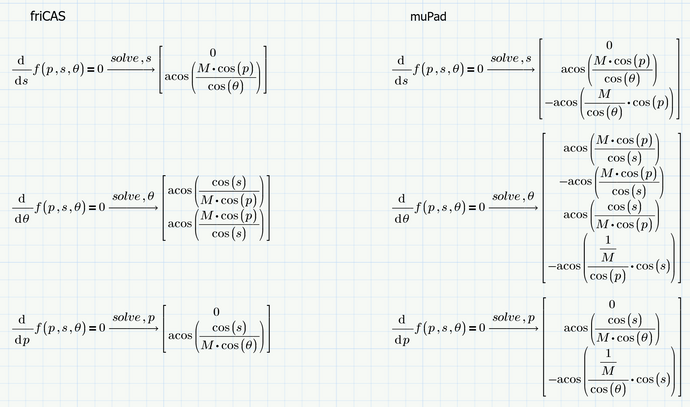
Next thing to wonder is why Mathcad gives 3 solutions for the p and s cases and 4 solutions for the theta case, while Prime gives you only 2 solutions for the s and theta cases (and who knows how many for the p case..).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This question can be solved by changing the calculation engine to "Legacy Symbolic Engine".
Then the two files have the same solutions, yet I don't know why this happens.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do, The 'legacy' symbolic engine of Prime 6 is the same as the symbolic engine in Mathcad 15 (MuPad).
The new symbolic engine in Prime 6 is a different beast (Fricas). It needs improvement...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But, did changing the labels help to solve your initial problem?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, the label issue has been solved. Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you now what's the difference between the 3 solutions?
Usually, we should have some specific limitation or range for each solution? but mathcad didn't specify these ranges, is there any way to look into these ranges?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you now what's the difference between the 3 solutions?
Usually, we should have some specific limitation or range for each solution? but mathcad didn't specify these ranges, is there any way to look into these ranges?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you now what's the difference between the 3 solutions?
Usually, we should have some specific limitation or range for each solution? but mathcad didn't specify these ranges, is there any way to look into these ranges?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To find that out, you'll have to look at the derivatives. For example, the derivative to p is:
This one is 0:
1. When p=0, becasue then sin(p)=0
2. When M*cos(theta)*cos(p)=cos(s), that is when cos(p)=cos(s)/(M*cos(theta)), thus when:
arcos(cos(p))=p=arcos(cos(s)/(M*cos(theta))). Since the cosine is a periodic function, there's an infinite number of solutions, so this happens for both positive and negative values of p with the same magnitude. The first set (closest to 0) is found and usually given by Mathcad. If you want all, you can add ",all" to the symbolic solve command.
What Fricas (The new symbolic solver) did was give you only the (first) positive solutions...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Some observations:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Trying to explain why muPad also adds -acos(...) to its solution and why this is correct in my opinion.
In mathematics arccos is NOT the inverse of the cos function, but rather is the inverse limited to the range from 0 to pi. The inverse of the cos function would have an infinity number of values for every single argument and therefore is not a function in the mathematical definition.
To solve the equation cos(x)=C requires x = arccos(C) but also x = - arccos(C) OR x = 2 pi - arccos(C). And of course you may add any integer multiple of 2 pi to any of these two "main" solutions.
friCAS seems to have its own interpretation and I definitely prefer the correct answers of muPad: