- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
mechanical "strange oscillator" problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
mechanical "strange oscillator" problem
Hi all
I have a mechanical problem, but i don't a have a mathematical skill to solve it, I hope that someone could help me👃
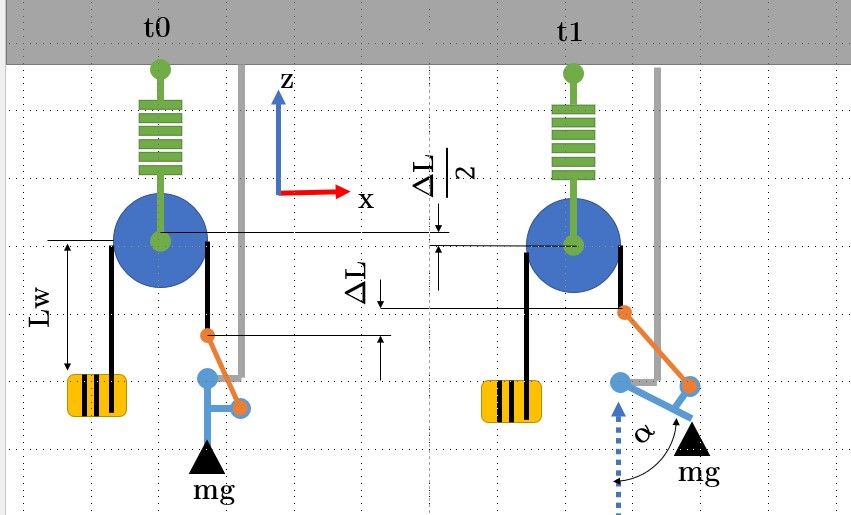
in first, see simplified drawing:
in yellow box , is a winch
- wire betwen winch and pulley (steel cable,the length is low, the elongation can be a constant, maybe )
- pulley connected to ground with spring
- wire betwen mechanical elbow and pulley (steel cable,the length is high, i need to use Hooke's law for evaluate elongation, and correct this to calculate good Lw parameter)
- mechanical elbow
- mechanical load mg ( for simplify what happens in mechanicel elbow, we consider un traction forces on wire node at elbow)
At t0 system at rest : it is as if the spring is a bar
At t1, the winch pulls to make an ordered value for alpha
Find Lw according to alpha angle, the object of the game is that the winch gives a Lw length which allows to maintain alpha angle according to the instructions (angle ordered)
What i feel : variable is a function f(x)=k(x) , here is a differential equation
I do not know, neither to pose this problem nor to solve it😓
this is above my skills, but it's very interesting
Anyone can help me ? I would like to learn how to solve this
- Labels:
-
Mechanical_Engineering
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i can add this comment:
At t0 we have a small load in wire. (prestressing)
This small load it make by traction spring, and it is nessary to avoid the cable goes out of the winch
Of course the winch is connected to a motor, and motor is connected to ground
the speed is low, and the system has time to equilibrate, it can be considered static I think
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Another one things, for show the scale, the wire cable diameter is 1 millimeter
and the systeme is small, the pulley (made with steel) diameter is 40mm and this thickness is 4 milimeter
I think that we can neglect the masses and the inertia of different part.
sorry for the multiple messages, but it seems that we can no edit the post
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should be able to edit your own posts, within about one day from first posting. Just go to the (three dots) menu in the upper right corner of the posting and select edit.
Regarding the topic: I wouldn't know where to start, but if you give me the (set of) differential equation(s) I'll be happy to help solve it.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your answer !
Unfortunately, i can't write this equation 😩
I think it's possible to reduce the problem to the equations of statics, and not to consider a dynamic system
If the point of view is : the system not move for each step time
In real world, it's possible to wait the system stabilisation between to step
I'll try to breakdown my system step by step to better identify the problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
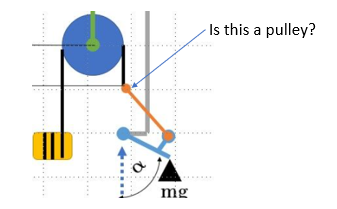
Need one more clarification:
What is the force reaction at this point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This point is not a pulley, is a hinge
and this hinge had a linear guidance on z_axis with ground
in the same way, the pulley (blue circle) have a linear guidance on z_axis with ground
i calculated reaction forces at this point in terms of alpha angle (resulting moment theorem)
and i finally, i find the lenght cable for alpha angle value 0° to 90°, it's no linear.
i translate my worksheet, after this, post it .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This point is not a pulley, is a hinge
and this hinge had a linear guidance on z_axis with ground
in the same way, the pulley (blue circle) have a linear guidance on z_axis with ground
If that hinge is constrained in x, then the tension in the cable is constant equal to the weight m g.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes I agree
But my problem is not the calculation of this force reaction.
My problem is behaviour of pulley and spring
if I consider the static system at each step of time
I must respect the first Newton's law : sum of external forces = 0
and my system (pulley + spring) subjected 3 forces
but for my spring F=ku
If F spring are lower or higher Fload (force reaction elbow), the alpha angle will vary
and the system will oscillate because of F=ku
and finally , the question is:
what is the offset of lenght cable winch to keep alpha constant
of course the hook law must be considered for the elongation of the cable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My point is this
If the angle of the weight does not alter the cable tension, then the spring extension length will not change (since the force on the spring is simply twice the cable weight.) You can wind the winch to slide the rig 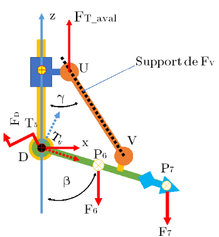
That does not mean that there isn't a resonant frequency--you have a mass suspended on a spring. But you don't have anything that will change the force acting on the spring.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Fred
i going to look you file...
But your premisces are not correct, it is normal that it is not understandable, because,
to simplify the problem I said only that the tensile force was variable.
In reality at P7 point in the drawing, we have another same elbow system.
I did not want to increase the problem, but I see that it is not a good idea
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
in any case, a big thank you to the community because your sheets are always a wonderful way for me to learn a lot of things