Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Error propagation - How can help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error propagation - How can help?
Dear Friends,
I know, I might know it, but I would like to ask.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Walter, hi Richard.
Now I figure why the mixture of the two theories. Probabilities for transform the standard deviation, and "error propagation" for transform parameters. Usually, parameters are take as exact values, without an associated error, so don't propagate his error. But if you call them as "fit", must to carry out error from the transformation. I guess that your formulation is correct, and in the last attach the values are corrects. I guess your job is complete now.
"Parameter" is an ambiguous word, which actually don't exist in pure math: are not variables, nor constants. Variables have derivative, then propagate errors, constants have null derivative, so don't. Parameters are ... any convenient thing. So, maybe propagate, maybe don't.
About Pythagoras (tanks for remember me how to write he in english) or absolute values, it is just a metric for the space. Check the Parseval identity, which looks like Pythagoras too, it came just from the "distance" between two "vectors" (functions in the vectorial space with infinite dimensions). The distance is defined as a integral, and that is the "dot product" between two functions (vectors in that space). When use the function minimize you're doing the same as a develop in Fourier series, for example: taking the "distances" from the exact value and minimizing the distances.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now I figure why the mixture of the two theories. Probabilities for transform the standard deviation, and "error propagation" for transform parameters.
Yes. Very good point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Richard, and Alvaro. But even my job is done there is still a question:
As written in http://pubs.acs.org/doi/pdf/10.1021/ed074p1339 if 1/v = f(1/S) then the covariance must be considered.
I have S(t) = f(v,k,t) which is the following solution from the ode:
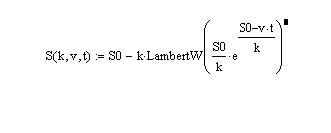
so I have to consider the COVARIANCE(b.m) which is COVARIANCE(1/v, 1/S) for one of the 3 cases.
How can the COVAR calculated form this functions?
After making a long internet recherche I found this here , which is the solution: It is a linear fit with error propagation for the same case as I have to deal with.
Thanks
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the final answer, done with the Excel Sheet and compared with the StdError Calculation with and without b-m Dependence.
![]()


- « Previous
-
- 1
- 2
- Next »





