Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A Classical Math Problem from a Classical Text (Differential Equation)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Classical Math Problem from a Classical Text (Differential Equation)
I have always had a problem deciding when I should use pencil and paper and when I should use Mathcad. After all Euler, Laplace and Fourier didn't have Mathcad. Recently I decided to look at some problems in the text "Operational Mathematics" by Ruel V. Churchill (2nd Edition McGraw-Hill 1958). Chapter 1 introduces the Laplace transform and shows how it can be used to solve certain differential equations. Attempting to solve one of the Examples in Mathcad quickly revealed the limitation of symbolic operator "parfrac" and the difficulty of solving differential equations with unusual initial conditions. I attach a Mathcad Prime 3.0 file describing my experience with "Example 4 p 21." This problem involves a third order differential equation with two values for Y(t), a value for Y'(0), but no value for Y''(0). To solve the problem and obtain a unique solution you must introduce a second variable Y''(0) = C. In the long run a combination of pencil and paper and Mathcad allowed me to reproduce Example 4. If you know an easier way I would like to hear about it. I have not yet attempted to work with Mathcad's ODE solvers.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's not extremely difficult to solve nth order ordinary differential equations with constant coefficients using Mathcad....
If you have Mathcad 11. Here goes:
Because (I assume) you don't have (access to) Mathcad 11, I add the pictures here.



And for those of you who do have access to Mathcad 11,I'll try to attach the sheet.
Which contains another axample: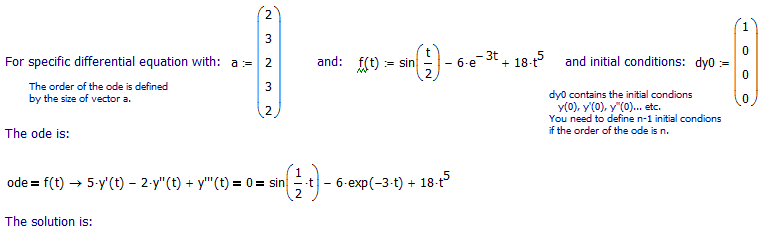
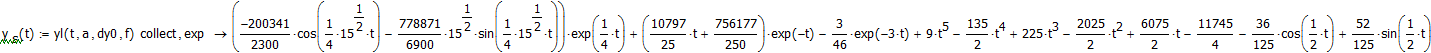
Hmm, cannot attach sheet, I'll post another thread with it here: A classical math problem: differential equations.





