Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to find correlation coefficient for 3-D polynomial regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to find correlation coefficient for 3-D polynomial regression
Hello all,
I'm working with a set of 3-D data (2 independent variables, 1 dependent value) in which I'm using the regress and interp functions to find a 3rd degree polynomial function to describe it. I have looked through the help and quicksheets and it appears that MathCAD does not automatically calculate the correlation coefficient for such a regression, so I'm wondering if there is something close in definition to a correlation coefficient to help me quantify the accuracy of the best-fit plane. I'm basically trying to quantify the fit difference between a 2nd-order polynomial, 3rd order, and 4th order.
Any help is appreciated!
Attached is a little eye candy of the a best-fit plane and superimposed data.

- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
[deleted content]
. Why not a spline fit for that surface.
Good idea to check thw qs for "Regress",
Minerr ... fit "
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm afraid I don't understand your post. I'm trying to figure out how to calculate the correlation coefficient for the best-fit surface, what's the problem? A best-fit spline doesn't help me because:
- The 3rd order polynomial fit is obviously an excellent fit. I need to quantify "excellent" however.
- I need to take the polynomial equation for the best-fit plane, and use it in the control software for this application. I can't give an interpolated spline equation to the control system!
As for your comment regarding the tags, I simply added some tags to make it easier to find this thread using a keyword search. That's what they're there for...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mech_Engineer wrote:
I'm afraid I don't understand your post.
Don't worry about it. Neither do I
- The 3rd order polynomial fit is obviously an excellent fit. I need to quantify "excellent" however.
Be very careful regarding what you mean by "quantify". You can use the correlation coefficient to judge the difference between the quality of different fits to the same data, but do not make the mistake of over interpreting it. For example, you cannot use it to compare different fits of the same function to completely different data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mech_Engineer wrote:
I'm afraid I don't understand your post. I'm trying to figure out how to calculate the correlation coefficient for the best-fit surface, what's the problem? A best-fit spline doesn't help me because:
- The 3rd order polynomial fit is obviously an excellent fit. I need to quantify "excellent" however.
- I need to take the polynomial equation for the best-fit plane, and use it in the control software for this application. I can't give an interpolated spline equation to the control system!
As for your comment regarding the tags, I simply added some tags to make it easier to find this thread using a keyword search. That's what they're there for...
If the 3rd order polynomial is your choice, then just plot the residuals to the fit and the data. My point about your tags is that up until now it does not help any visitor whereas at your 2nd visit you have no work sheet. Eventually if your project is interesting, some collab might just generalise and repost under another thread, then tag appropriately. There is no "best fit spline" ,spline surface only and the most common Mathcad splines are cubic !
Attach the sheet, that will shorten the discours.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To the SsE already suggested, add:
1. Standard error estimate
2. Leverage
3. "Studentized" residuals
4. Mathcad built-i corr(vx,vy)
5. Constant error variance,
6. Durbin_Waton ststistics,
7. Pearson correlation
8. Euclidean error
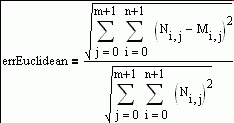
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See here:
(long URL!!!)
But I think that's overkill. If you want to compare the difference in the quality of different fits to the same data all you really need is the sum of the squares of the residuals (i.e. sum[(z-fit)^2]).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think I'll just sum the squares of the residuals. I was hoping there was a built-in function that I could call, but alas there is not.
Thanks for the help Richard.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mech_Engineer wrote:
I think I'll just sum the squares of the residuals. I was hoping there was a built-in function that I could call, but alas there is not.
Thanks for the help Richard.
The Mathcad built-in ERR is paired with Minerr
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you should be careful about using polynomial fits, particularly if there is no rational physical explanation for using a polynomial, and particularly if there is any sort of noise in the data.
Philosophically, regression attempts to "thread" the data, i.e., picking the smooth path that is equidistant from all data points as an ensemble. A polynomial fit will undulate to miinimize the distance function to the points, so while a 3rd order might an "excellent" fit, a 4th order will result in even lower residuals, and a 5th order will result in still lower residuals. In fact, it may well be that a 3rd order is already twisting to minimize the residuals, and will not necessarily be appropriate for a fitting function that is used to predict performance.
TTFN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Reading the new and long description from the collab and in reference to Solidworks, the problem is ill posed from the concept. The X Y planes aren't linear from the description and the problem is to put in numbers for the motions in the 3 directions, each direction being meshed fine enough. Then correlation does not apply. If Solidworks builds a 3D solid, it builds from some internal data it calculates, just make it finer with more points and plug it to the machine tool that will fabricate the piece. The project can be described otherwise as 3D NURBS to be started from scratch. It could simply be a Catmull-Clark spline that Mathcad can do without Solidworks. The project resumes to getting the Solidworks data sets, meshed fine enough and pass the data to a CNC or get Mathcad do the Solidworks.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the feedback, I'm hoping the polynomial will work for this particular application (but it's possible to see some of the undulating errors you describe in the error plots). The data is positioning output from a Solidworks motion study, so there's no noise in it.
4th degree polynomial error plot (only valid at data points):

Basically I have a tilt-rot table that I'm positioning using two linear actuators attached to it; I need an equation that describes the actuator lengths as a function of tilt and rotation angles of the table. I've thus far been unsuccessful in describing the geometry analytically, so I've gone to using Solidworks and MathCAD to develop an approximation. Due to the required accuracy of the table I need the error of the approximation formula to be less than 0.010" within the space I'll be positioning, which based on my error calculation necessitates a 4th degree polynomial (results in a Root Mean Error of .009", although the error in some areas is as high as .020"). Unfortunately, a 4th (or even 5th) degree fit results in not only a huge equation to put into the control system, but the points used in my regression are not evenly distributed accross the motion space meaning I only "know" I'm accurate at the data lines I'm regressing, and the fit may be undulating between them. I think my next step to minimize this problem is to try getting a more random distribution of points accross the motion space.
I've attached the MathCAD sheets from both the regression, as well as my original attempt at formulating an analytical symbolic solution using a system of equations (25 unknowns) and a Solve block in MathCAD. I suspect the symbolic solution is not solving because I have not yet fully constrained the system; the one I'm missing is "Line DE is always parallel to a plane that is at a known angle from plane ABC," but I haven't figured out how to describe that in an equation for the solve block.
Any feedback you have on either sheet is most welcome. It's nice to get some outside advice ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You seem to be at a point of not understanding and not possibly reverse engineering the material you are passing . The CNC will fabricate from a data set, a data set that can come from a mathematical function like the breather or a set of coordinates in the space. The Catmull-Clark being is convex to the hull, no correlation will apply except for you to determine from experimental runs and how fine the meshing must be. Hope some collabs can help, on my side the project does not even exist yet as you have no data set in the space and no function.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry about that I forgot the Worksheet is linked to an Excel file for the values. I uploaded an updated Worksheet and the excel file it pulls the data from, so as long as you download both files in the same directory it should work.
I can tell that we're communicating accross a language barrier, but I think I'm getting that I can do a cubic spline interpolation which will allow a polynomial interpolation through the data points I have, rather than a regression which does not actually pass through all of the data points provided. I'll try the cubic spline and see if it works for me, thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Reply from Mechanical Engineer [Mona: I deleted the original message by mistake]
Jean,
You are completely misunderstanding the problem I'm trying to solve, this has nothing to do with interpolating a 3-d geometric shape, or reverse-engineering a competitor's design. You're right that this is a proprietary company design so I can't post any pictures of it, but I've described it's essence in some detail.
Again: I have designed a dynamic pointing system in Solidworks. It is similar in operation to a hexapod actuator (for example this one: http://www.physikinstrumente.com/en/products/primages.php?sortnr=1000770) except that instead of 6 actuators to achieve 6 degrees of freedom, I am only utilizing 2 actuators for 2 degrees of freedom (the other 4 degrees of freedom are constrained by a custom universal joint assembly). The two actuators can adjust the table's pointing up-down and left-right.
Solving the kinematic equation that describes the actuator lengths as a function of the pointing system's two angles is a difficult proposition, and I was unable to solve it (the attempt is contained within "Kinematic Equation Development 2.xmcdz"). So, rather than waste more valuable time trying to get the analytical equation solved, I decided to instead use Solidworks' Motion Analysis package to output data points that describe the two actuator lengths as a function of the positioning system's two angles- theta and phi.
In this thread, we have only been looking at the Left-hand actuator (denoted as sub-LH in most of the MathCAD sheet). Exporting all of the positioning data from Solidworks to Excel gives me a point cloud that I then have to describe using an equation. I have solved it using a 3rd-5th degree polynomial fit, and that seems to have worked. The regression analysis can be seen in the other attached mathcad sheet and excel spreadsheet.
The point of this thread was just asking if MathCAD finds a correlation coefficient for a 3-d polynomial regression. It does not, so I have used an error estimate instead. Thread solved.


