Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Please help! Variable should be scalar or matrix?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please help! Variable should be scalar or matrix?
Hello guys,
I see there are a lot of clever people on these forums.
There is an assignment I have to hand in real soon and I am stuck on a question which asks me to solve a 2nd order differential equation using laplace and then plot it on a graph.
However the problem I am having is that the question asks for one of the initial conditions to be of a range. Thus the graph must have 6 lines.
All my forumlas work for when y0 is a single number, but as soon as I make it into a range. I do not get any plot on my graph at all.
y0 = 0,1,2,3,4,5
Can someone please help?
All I need it to do is plot all the 6 lines for different values of y0
I have attached my file
it is saved in mathcad 11
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, it looks like you are not quite sure about variables and functions and what happens at a laplace transform. You really should clean up your variable names and function definitions. You get a result for a specific y0, but that's only because Mathcad's symbolic sometimes is quite generous and forbearing.
So set y0:=1 for a while and lets begin with varD. Its not a variable but a function of time, so please address it with varD(t). Aren't the various function f with different meaning not even confusing for you yourself? The laplace transform of a function in time domain is a function in frequency domain with a complex argument, usually named s. You may name that variable d instead but you would have to type "laplace,t,d" to do so. I'd rather stay with s and call the new function F(s). So you have F(s):=varD(t) laplace,t,s --> Adding t and s is not necessary though, as those variables are supposed to be named that way. As far all red should be gone and you should see F(s) express in s to the right of the arrow.
In the solve block (I would have used the symbolic solve for that) you sure would write F(s) on the rhs of the equation and as you solve for Y and you are in in the complex s-domain you get a function in s. So please call the outcome of find Y(s) and not f(t)!. Gone so far you should see the function term of f(t) after invlaplace and all red indicating errors should be gone.
Now for the reason of your post, varying y0. This does not work with a range variable (wrong, we will do it with a range variable, but not the way you tried it)
The goal is that the solution f(t) is not only dependent of t but also of y0. That way using f(7,t) should be the function for y0=7. We have to add y0 as parameter/argument in the above calculations wherever needed.
First delete the assignment y0:=1 on top. laplace transform does not deal with y0 so we don#t change anything there. But Y(s) is dependent on y0 so you have to change it to Y(y0,s) two times. The result of invlaplace is also dependent on yo, so we call it f(y0,t). We are already finished but you still don't see a graph.
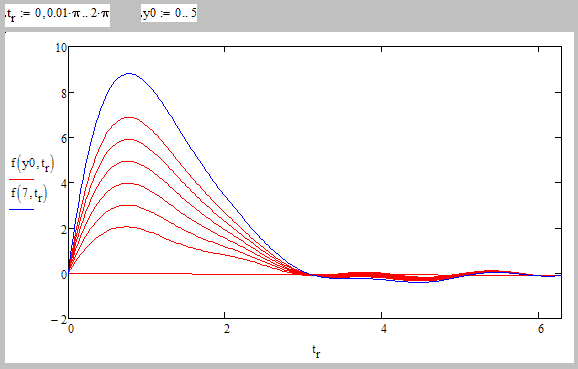
fist you should rename your range variable y to t. That's not really necessary but makes sense, doesn't it? Now in your graph change y to t and f(y) to f(2,t). You will see the graph for y0=2. I assume you know how to plot multiple function in a single xy-plot by separating the function names with commas. That way every graph could be of different color. But then you may consider to graph all 6 graphs with only one function name at the abscissa, That way all sic graphs would have the same color. define a range variable on top of the graph y0:=0..5 (you may omit the ,1, as Mathcad assumes step 1 if not otherwise stated.
Then the only graph you need to plot would be f(y0,t) and you should see all six graphs.
Try to implement that lengthy explanation and if you feel unsure come back here.
In the screenshot I named the range variable for plotting t.r in case you need a free variable t for further calculations.
In addition to the six graphs you are asking for I included in blue the one for y0=7.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, it looks like you are not quite sure about variables and functions and what happens at a laplace transform. You really should clean up your variable names and function definitions. You get a result for a specific y0, but that's only because Mathcad's symbolic sometimes is quite generous and forbearing.
So set y0:=1 for a while and lets begin with varD. Its not a variable but a function of time, so please address it with varD(t). Aren't the various function f with different meaning not even confusing for you yourself? The laplace transform of a function in time domain is a function in frequency domain with a complex argument, usually named s. You may name that variable d instead but you would have to type "laplace,t,d" to do so. I'd rather stay with s and call the new function F(s). So you have F(s):=varD(t) laplace,t,s --> Adding t and s is not necessary though, as those variables are supposed to be named that way. As far all red should be gone and you should see F(s) express in s to the right of the arrow.
In the solve block (I would have used the symbolic solve for that) you sure would write F(s) on the rhs of the equation and as you solve for Y and you are in in the complex s-domain you get a function in s. So please call the outcome of find Y(s) and not f(t)!. Gone so far you should see the function term of f(t) after invlaplace and all red indicating errors should be gone.
Now for the reason of your post, varying y0. This does not work with a range variable (wrong, we will do it with a range variable, but not the way you tried it)
The goal is that the solution f(t) is not only dependent of t but also of y0. That way using f(7,t) should be the function for y0=7. We have to add y0 as parameter/argument in the above calculations wherever needed.
First delete the assignment y0:=1 on top. laplace transform does not deal with y0 so we don#t change anything there. But Y(s) is dependent on y0 so you have to change it to Y(y0,s) two times. The result of invlaplace is also dependent on yo, so we call it f(y0,t). We are already finished but you still don't see a graph.
fist you should rename your range variable y to t. That's not really necessary but makes sense, doesn't it? Now in your graph change y to t and f(y) to f(2,t). You will see the graph for y0=2. I assume you know how to plot multiple function in a single xy-plot by separating the function names with commas. That way every graph could be of different color. But then you may consider to graph all 6 graphs with only one function name at the abscissa, That way all sic graphs would have the same color. define a range variable on top of the graph y0:=0..5 (you may omit the ,1, as Mathcad assumes step 1 if not otherwise stated.
Then the only graph you need to plot would be f(y0,t) and you should see all six graphs.
Try to implement that lengthy explanation and if you feel unsure come back here.
In the screenshot I named the range variable for plotting t.r in case you need a free variable t for further calculations.
In addition to the six graphs you are asking for I included in blue the one for y0=7.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks so much that was VERY helpful.
I got this problem sorted now.
You guys really know your stuff.
God bless
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





