Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
The problem with boxes - 1, 5, 21...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem with boxes - 1, 5, 21...
We cut out from one square sheet (cardboard), four small squares and make a cross-shaped piece out of the box. Then we cut out of four small square sheets sixteen more small squares and make them into new boxes and so on to infinity. What will be the maximum amount of an infinite number of boxes?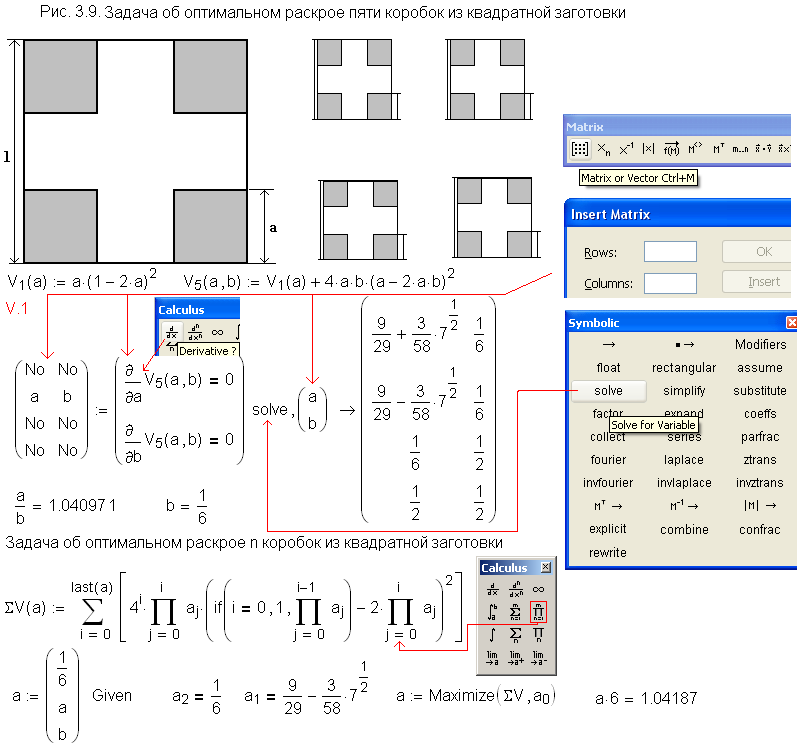
- Labels:
-
Algebra_Geometry
- Tags:
- group discussion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
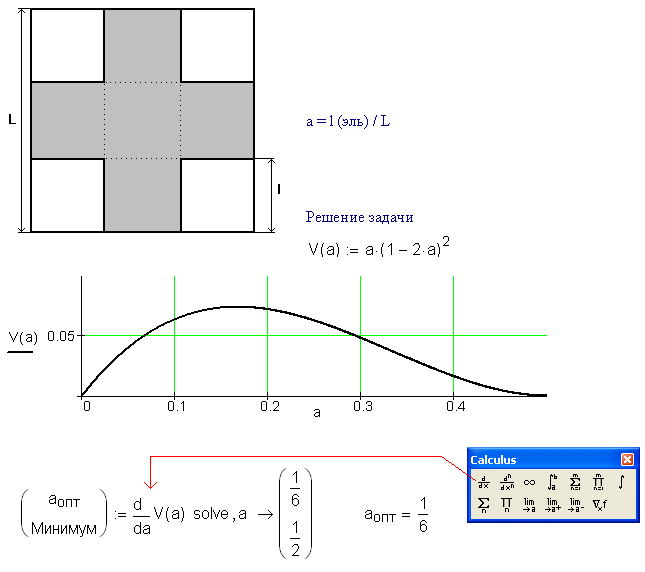
One solution for a one box:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the total volume is given by V=a(1-2a)^2/(1-4a^3), where the value of 'a' to give maximum volume is 0.174 and the corresponding value of V is 0.076.
See attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan!
What can you say about this solution:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting recursive relation for 'a'. Can't see where this particular one comes from! No real need for intermediate results here of course; just set 'a' to be the same on both sides and solve for a to get the infinite recursion value immediately.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Interesting recursive relation for 'a'. Can't see where this particular one comes from!
I can't see too ![]()
One reader of first my book on Mathcad (see the Preface >>>) has sent me this solution without any description (may de he was legendary Tom Gutman ![]() )
)
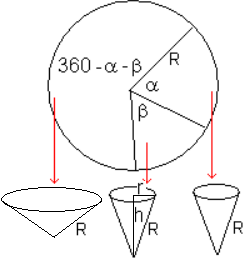
And other same problem! How many cones with max sum volumes we can do from one circle workpiece?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a "starter for ten". Numerical only. I've assumed each segment angle bears same relationship to what remains as first segment angle bears to whole cirlce. I haven't proved that this leads to the maximum volume (it might not!).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Here's a "starter for ten".
Ten!?
Sorry, Alan!
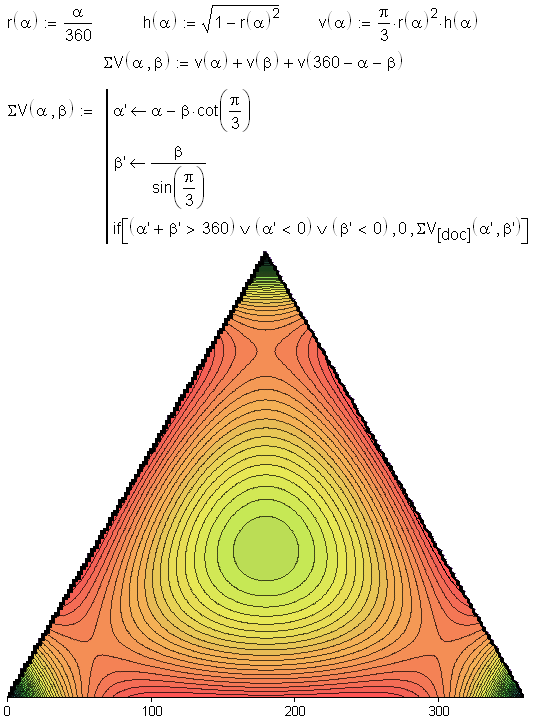
I think we can have only two cones with max sum volume.
The sum volume is less with 3-d cone!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the infinite cone assumption is easily outmatched here.
Alan
PS The phrase, "starter for ten", comes from a quiz show in which contestants have to answer a "starter" question that gives them 10 points if they answer correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
PS The phrase, "starter for ten", comes from a quiz show ...
OK!
We say in Russia in same case "dance from the oven"!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've figured out where the recursion relation for the boxes comes from:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Tom Gutman ![]()
And what about cones from the round workpiece?!





