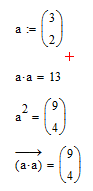Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Evaluate values in two Matrices
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Evaluate values in two Matrices
How do I evaluate each element in two matrices of equal sizes (4 rows x 5 columns) and then return the maximum value into a new matrix? I want to evaluate each element with the corresponding element on the second matrix and produce a new matrix. Thank you in advance for your help with this!
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Following on from Werner's example the code could be contained in a simple nested for loop program.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So if we go into programming, lets make it complete and create a utility function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nicely done ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Impressive! Thank you both for your help with this.
I am still doing something wrong. I have attached part of my work to see if you could help me identify the problem.
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have fixed the matrix comparison, please note the changes I made. You do not need to add the subscripts when defining the a matrix that way.
Can you please elaborate on what you are trying to do with t.plate.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ad definition of L.c.325.x: You are trying to divide a 4x1 column vector by a 1x5 row vector and you really expected that to work? Thats brave! What did you expect to get?
Is the 4x5 matrix what you expected and what you need? If yes, congratulation - you found a nice way to achieve what otherwise would have required some programming.
A quick look in the theory of vectors and matrices will tell you that you cannot divide anything by a matrix. It will also tell you that you can only take the inverse of a sqare matrix, not of an 1x4 nor an 4x1 vector. So why did it work in your sheet for the (transposed) 4x1 vector? Explanation is "implicit vectorization". Whenever you evaluate an expression in Mathcad containing vectors (and in MC thats only column vectors) and you use an operation which is not defined for vectors (like exponentialization) but only for scalars, Mathcad applies implicit vectorization. That means one by one every element of the vector is inserted in the expression (not the whole vector) and the expression is evaluated. The various results are collected and returned in a vector. So when you transposed t.plate, making it a column vector and applied the operator ^-1 on it, it is not interpreted as the inverse of a matrix (t.plate transposed is not square) but as the scalar reciprocal value. This is not defined for vectors so Mathcad vectorizes and takes the reciprocal value of every element of the vector t.plate.transposed.
See the following examples:
a*a: is the vector scalar product. Thats how multiplication is defined for vectors
a^2: squaring is not defined for vectors! So Mathcad applies vectorization and squares each vector element singly - the result is again a vector
The last one is again a*a but this time explicit vectorization is applied and so Mathcad is forced to work on the elements one by one.

EDIT: Here is away to get the same matrix you got - again no programming but using range variables which may give you better control and understanding of the outcome. Note that to access the elements of t.plate we have to use both matrix indices as its not a (column) vector:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
A quick look in the theory of vectors and matrices will tell you that you cannot divide anything by a matrix. It will also tell you that you can only take the inverse of a sqare matrix, not of an 1x4 nor an 4x1 vector. So why did it work in your sheet for the (transposed) 4x1 vector? Explanation is "implicit vectorization". Whenever you evaluate an expression in Mathcad containing vectors (and in MC thats only column vectors) and you use an operation which is not defined for vectors (like exponentialization) but only for scalars, Mathcad applies implicit vectorization. That means one by one every element of the vector is inserted in the expression (not the whole vector) and the expression is evaluated. The various results are collected and returned in a vector. So when you transposed t.plate, making it a column vector and applied the operator ^-1 on it, it is not interpreted as the inverse of a matrix (t.plate transposed is not square) but as the scalar reciprocal value. This is not defined for vectors so Mathcad vectorizes and takes the reciprocal value of every element of the vector t.plate.transposed.
See the following examples:
a*a: is the vector scalar product. Thats how multiplication is defined for vectors
a^2: squaring is not defined for vectors! So Mathcad applies vectorization and squares each vector element singly - the result is again a vector
The last one is again a*a but this time explicit vectorization is applied and so Mathcad is forced to work on the elements one by one.
Well done with the explanation Werner. I think Mathcad should document the theory of vectors and matrices a little better.
For example how would one know that a function is not defined for vectors?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For example how would one know that a function is not defined for vectors?
Thats math knowledge, not Mathcad specific.
But vectorization is Mathcad specific and needs explanation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
For example how would one know that a function is not defined for vectors?
Thats math knowledge, not Mathcad specific.
I still think Mathcad should highlight that functions such as the natural logarithm is not defined for matrices and will need explicitly vectorizing when applied to arrays.
But vectorization is Mathcad specific and needs explanation.
I might create a document with the information I have available.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I still think Mathcad should highlight that functions such as the natural logarithm is not defined for matrices and will need explicitly vectorizing when applied to arrays.
No, its the other way round - the logarithm of a vector would NOT need explicit vectorization but would be automatically vectorized. Furthermore in Mathcad vectorization only works for (column) vectors, not for other matrices.
There are not much operators or functions which are defined to work on vectors (+,-,*, absolute value), so most of the time Mathcad would apply implicit vecorization. Nevertheless I would suggest to use explicit vectorization in any case to be on the safe side.
Implicit vectorization can lead to confusion as in case of this thread as Jennifer seems to have thought she calculated the inverse of a 4x1 matrix and asked why she was not able to do the same with a 1x4 matrix.
It might be an idea to prohibit automatic vectorization (customizeable per option hopefully) but its often convenient to have it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
No, its the other way round - the logarithm of a vector would NOT need explicit vectorization but would be automatically vectorized. Furthermore in Mathcad vectorization only works for (column) vectors, not for other matrices.
I actually meant for the 'absolute operator' as you correctly specified.
Werner Exinger wrote:
There are not much operators or functions which are defined to work on vectors (+,-,*, absolute value), so most of the time Mathcad would apply implicit vecorization. Nevertheless I would suggest to use explicit vectorization in any case to be on the safe side.
That is good advice. I have just checked a selected few operators on the calculator:

Of those I checked it was only the multiplication and absolute functions which do not implicitly vectorize. I cannot see the logic.
I agree with your 'customizeable per option' suggestion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of those I checked it was only the multiplication and absolute functions which do not implicitly vectorize. I cannot see the logic.
Th logic is the mathematics of vectors itself. There is not that much you can do with vectors (which doesn't mean vectors wouldn't be important). But multiplication and absolute value are mathematically defined to yield a scalar and so Mathcad has to act accordingly.
I could live with an errormessage "the operand has to be a scalar" when I enter log(v), etc., but I would nevertheless prefer having the choice if I want implicit vectorization done or not. As for the absolute operator it would be possible to add a third variant to the two we already have in the right click menu (MC 15 and below), but honestly I am pretty satisfied with the way Mathcad handles it at present.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Of those I checked it was only the multiplication and absolute functions which do not implicitly vectorize. I cannot see the logic.
Th logic is the mathematics of vectors itself. There is not that much you can do with vectors (which doesn't mean vectors wouldn't be important). But multiplication and absolute value are mathematically defined to yield a scalar and so Mathcad has to act accordingly.
Thanks for the explanation that has cleared it up for me.
Werner Exinger wrote:
I could live with an errormessage "the operand has to be a scalar" when I enter log(v), etc., but I would nevertheless prefer having the choice if I want implicit vectorization done or not. As for the absolute operator it would be possible to add a third variant to the two we already have in the right click menu (MC 15 and below), but honestly I am pretty satisfied with the way Mathcad handles it at present.
Another good idea.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
A quick look in the theory of vectors and matrices will tell you that you cannot divide anything by a matrix
One example http://communities.ptc.com/message/245695
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wouldn't have expected anything else, but I agree it can be confusing to an unexperienced user.
Looking at your file I just realize that Prime seems to allow "vectorization" for non vectors, too - thats new, I wasn't aware of this. Vectorization of the absolute of the square matrix |A2-A1| as you did at the end of that file won't work in MC15 and below.
EDIT: I just investigated and explicit vectorization can now (in Prime) be done with any matrix, not just column vectors. Not bad!
But automatic implicit vectorization will still only be done for column vectors. May be called slightly inconsistent.