How to model bimetal beams in Simulate Structure

[tleati]

Hi,

I have to perform a structural simulation on a frame with beams idealization, and one beam is composed by two different sections made of two different material (two metals). To semplify the explanation, let's take this example, where the central section has two tubes of different materials one into the other :

I am wondering if and how could I do this. 

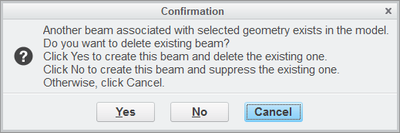
If I apply two different beam idealizations (with different section and material) to the same entity (sketch curve in my case), the software asks me if I want to delete or suppress the existing one, since it cannot overlap them:

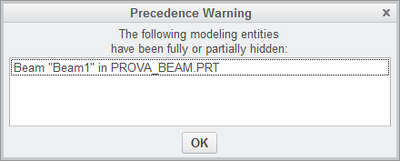
If instead I try by defining two overlapping curves in the sketch, and then assign one profile to one and the other to the other, this windows appears:

as if it has to "hide" (don't know what it exactly means) one of the two beams.

By attempting then to start the simulation, it seems that it makes no difference whether there is the second section or not. (as if it had been ignored by the software).

Anyone has done this before and/or knows how to perform this kind of modeling?

Thanks

[jmoradiya]

Hello tleati,

As far as I understood , you want to simulate one beam with another overlapping beam with different section and material. right?

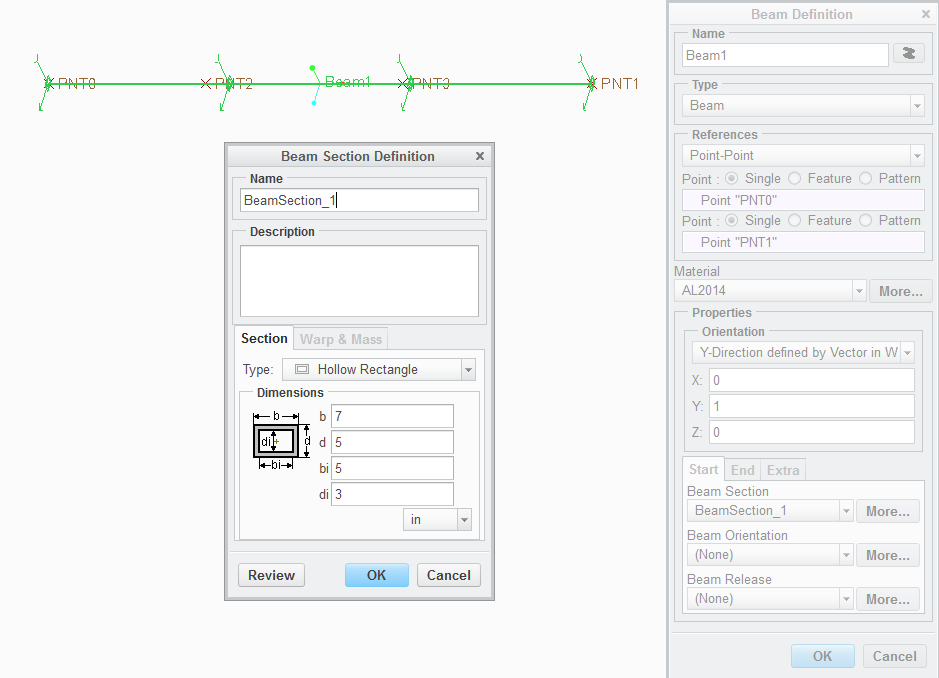
then it is possible by selecting references as 'Point-Point' in Beam Definition dialog box.

For example, you want to simulate one beam Hollow rectangle section_1 from PNT0 to PNT1.

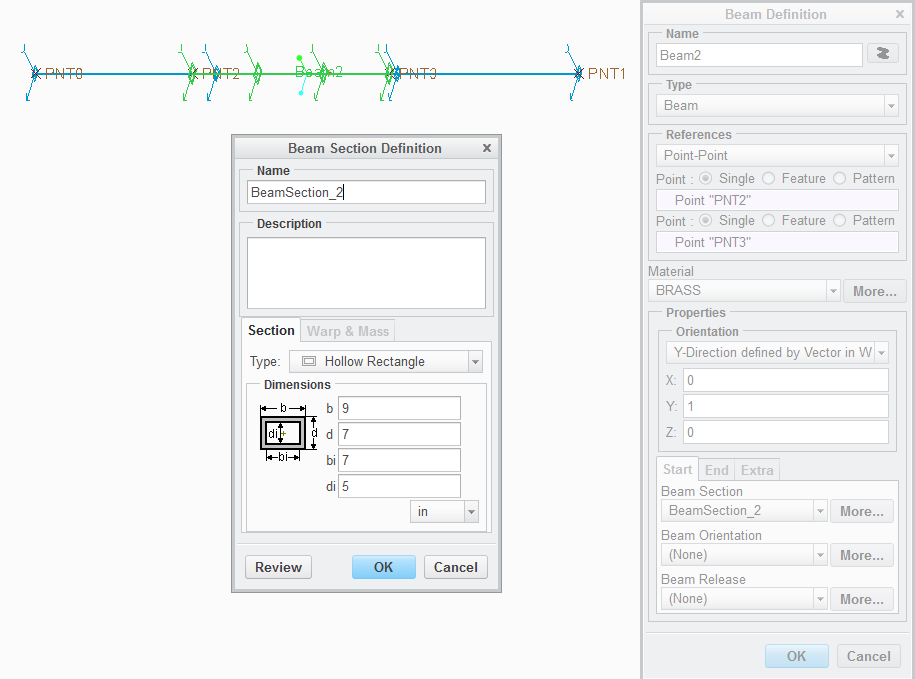
then second beam would overlap on first created beam with small length and larger section_2 from PNT2 to PNT3.

 As you can notice from picture both are defined with different materials.

At the end result would be look like, see picture below...

By defining this, I did not get any warnings. Herewith I have attached .prt file.

Do you exactly want this?

Regards,

Jignesh Moradiya

[tleati]

Hi Jignesh,

thanks very much for your detailed reply.

I tried to perform what you indicated and indeed it does not make any error in the phase of beam definition, but the analysis isn't starting at all. I tried two cases:

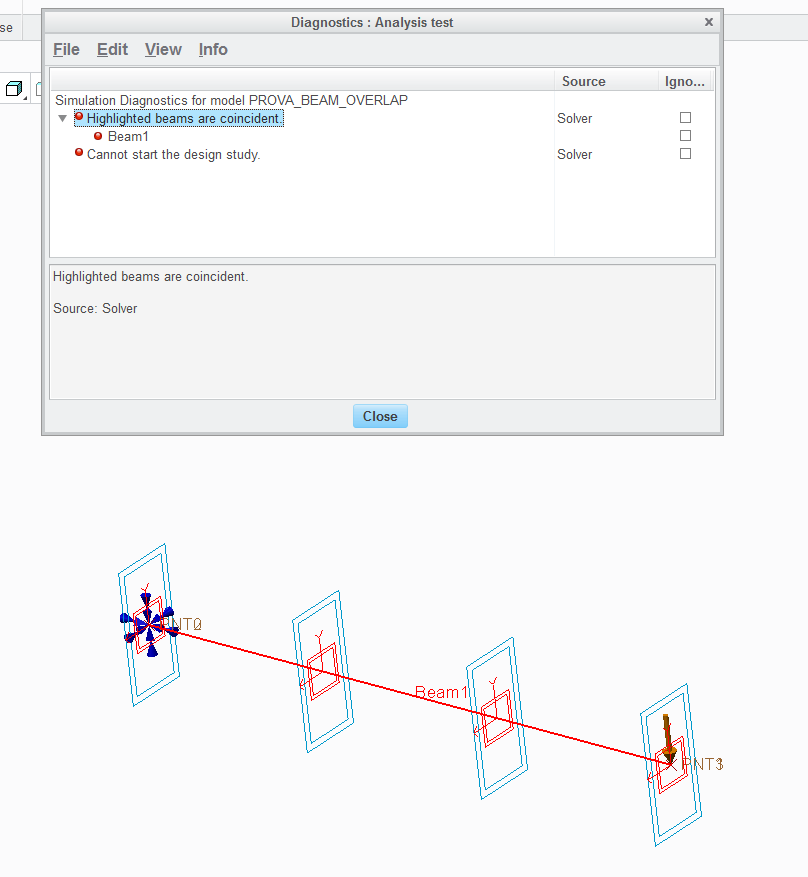
1) points 2 and 3 coincident respectively with point 0 and point 1 (overlapped beams are of the same length, that is what I need in this specific case).The error in this case is the following:

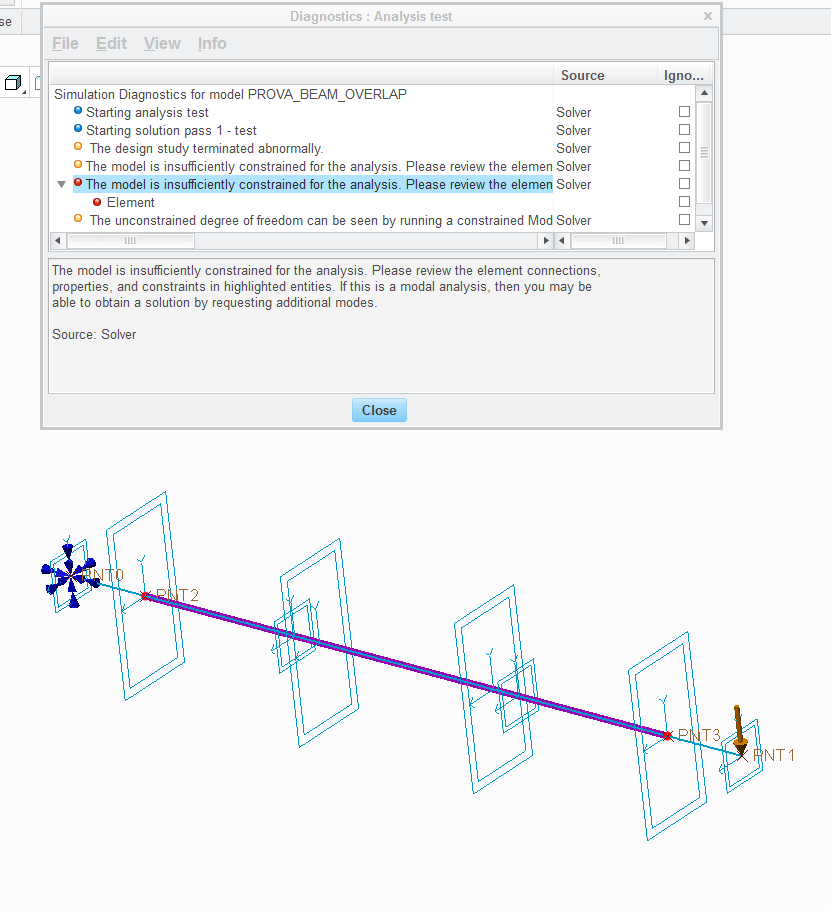
2) points 2 and 3 are not coincident with point 0 and point 1 (so the two beams overlap just on the length of the second beam, that is the case you showed and that would be usable anyway in my analysis also).The error in this case is the following:

Also, I tried to open your file but I can't, the software says it "can not be retrieved". (Probably due to different versions of Creo?I have Parametric 2.0 M110).

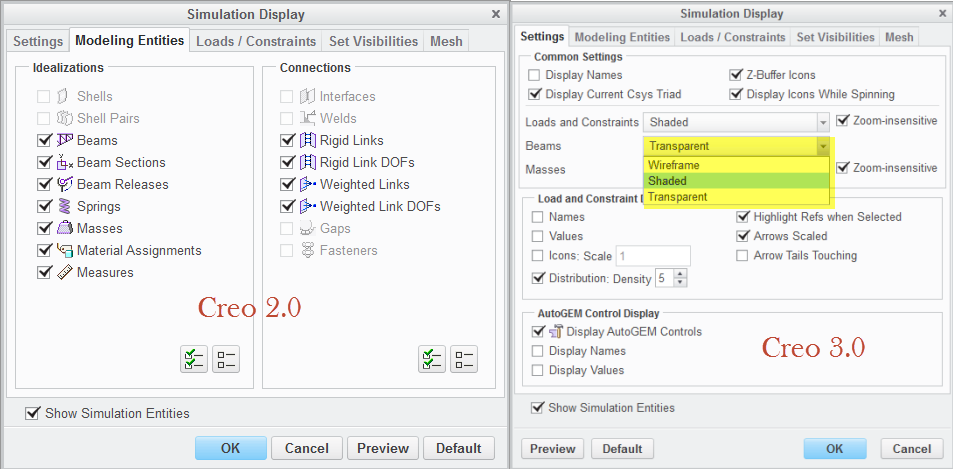
Another thing, how did you do to show the two beams with the (blue) shading, as I can see in your last image? It's comfortable to see.

Thanks

Tommaso

[Jignesh]

Hello Leati,

Yes, in 2nd case, you would get an error "The model is insufficiently constrained"  because the shorter beam has no connections with the longer beam(which is constrained and loaded). 

To answer your last question about blue shading of beam idealization, with help of Simulation Display, but it is not possible in Creo 2.0.

for example,

I have no idea how can be 2 beams (Beam Idealizations) connected here. But if you try with 3D bimetal beam in which both beams have bonded interface, can be successfully analysed. I have created one 3D example with PTC Creo 2.0, refer to attached file.

Can I ask, is it necessary to use beam idealizations?

Regards,

Jignesh Moradiya

[tleati]

Hi Jignesh,

yes in fact it's because the two points 2 and 3 are not connected with the other beam, so also in your example they lead to a failed analysis if I got it right, don't they? Usually Simulate, whenever you plot coincident edge vertexes, automatically cointrains the ends but not in this case evidently.

It's a pity it's not available in Creo 2.0, anyway when we go upgrading will be there...

And for you last question, yes I absolutely need to calculate with beams because it takes far less computing time (and effort) than the 3D.

Thanks very much for your help!

Tommaso

[skunks]

example attached (creo2_m080):

regards

paul