Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Re: how to retrieve ALL csys parameters
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
how to retrieve ALL csys parameters
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
how to retrieve ALL csys parameters
Every CSYS is mathematically defined in space by 6 parameters.
Is it possible to retrieve these 6 parameters (XYZ-translation + XYZ rotation) in Creo?
The XYZ translation is easy: it's just a measurement feature.
But the rotational parameters are not that simple.
Does anybody knows how to do this?
Some background:
I have a CSYS, somewhere in a complex assembly.
It is defined by a long chain of features and dependencies, interconnected with parameters and relations.
At the end of the road, I would like to know the exact position of this CSYS, with reference to the base CSYS.
With these 6 parameters, I should be able to create a new CSYS, referenced to the base CSYS, and equal to the original CSYS.
Any help would be greatly appreciated.
Jeroen.
Solved! Go to Solution.
- Labels:
-
Assembly Design
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok,
problem 'solved'...
I used the information provided by Antonius, David and Eric, and I mixed them into a solution.
I now have a piece of code/features/measurements where I can make a UDF from to use in my components.
It's a bit more complex as imagined beforehand, but it works like a charm now.
If you are interested, I enclosed the part. All information to create a new CSYS is in the last feature (EULER_ANGLES)
Thank you all!
PS: I got in touch with someone from PTC, but they told me it wasn't possible in any way to get this information in an easy way, unless you should program it with pro/toolkit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you tried a transform measure? Creo 2.0: Analysis [tab] -->Meausure [down arrow] --> Transform. Pick two coordinate systems using CTRL and it will give you the XYZ distance and rotation matrix. Hopefully that gets you what you want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can gather the information on the coordinate system. The info window has the designated dimension values.
More detail and the data is provided in the middle data on the UI if you scroll it.
Remember that the CSYS can have spherical or cylindrical coordinates. Not sure if this affect the stored information.
I did finally resolve another issue I've been having with defining planes... how one can create a plane normal to the screen?
Turns out you can do this with a CSYS from which you can make planes.
I often find the need for this in presentations for saved view orientations.
Now I know I can save a CSYS to that orientation easily ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks both.
The way I first tried it, is based on Antonius' post: Create a new CSYS (1) on top of the one you would like to get the information from, and in the orientation tab, select "orient by selected CSYS axes". Here you select the reference CSYS.
Afterwards, create feature relations (2) for this new CSYS to read the 6 location parameters, and put them in feature parameters.
These parameters I can use to create a new CSYS (3) directly referenced to the base CSYS.
This works, but if I change anything in the chain that alters the position of the measured CSYS, the new CSYS in step (1) would not update. I really need to have this to update.
The method based on Erics' post seems to be better in a way that this solution would update if something would change and the position of the first CSYS alters. But it's not clear to me how to transform the 4x3 transformation matrix into useful parameters to create my new CSYS.
Any thoughts?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure what the "4" is in the 4x3. I see the stored data as 3x3... XYZ and rotation about XYZ.
Since my original example is based on the default CSYS, this should remain constant. By changing any of the 6 parameters that controls the new CSYS, anything associated to it should likewise change. So therefore, if you reference a third CSYS from the second, that means the third CSYS should reorient maintaining the same values. Technically, you should be able to build and entire part based on the second CSYS and have the entire model follow any change you make in the 6 values. Again, you will never alter the default CSYS, just the second one. And you can base everything else on that second CSYS.
The implications can be significant in at the assembly level where you can apply geometric equations to the 6 values. They can exist anywhere in space in any orientation. Furthermore, the CSYS dialog does allow for Cylindrical and Spherical coordinates from the default CSYS. I just don't think it stores them this way... it is merely an interpolation matrix in the UI that you would have to reverse engineer to use them in relations as a geometric formula.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Okay, happily I am wrong about the interpolation. A CSYS defined by spherical coordinates from the default CSYS will maintain a radius (linear) and 2 angles for location, and 3 angles for orientation at the new location.
D18, 19 and 20 are the location, and 12,13, 14 labeled X, Y, and Z are the orientation angle in relation to the default.
Of course, cylindrical will be linear values for radius and Z values and angle for location.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I included an example: http://kvisit.com/S64CfAw
In the example you can see :
- the BASE_CSYS
- several INTERMEDIATE_CSYS (fixed in this example, driven by parameters in reality)
- the FINAL_CSYS : the resulting CSYS.
You can imagine this situation as being several CSYS of a telescopic robotic arm with several wrists. The next CSYS is depending on the previous. Angles and/or translations possible between the intermediate CSYS.
The FINAL_CSYS would be the claw.
I now need the absolute reference of the FINAL_CSYS, measured from the BASE_CSYS. This measurement needs to be up-to-date all the time, even when parameters of the INTERMEDIATE_CSYS should change.
In the example I included a CSYS called NEW_CSYS_REF_TO_BASE. This would be the exact thing I need, except if you alter something in an INTERMEDIATE_CSYS, this NEW_CSYS_REF_TO_BASE will not update accordingly. It has lost it's references. So, this solution cannot be used.
--------------------------------------------------------------------------------------------------------
Another approach would be a measurement (transform). Doing this, I get a 4x3matrix containing a 3x3 rotational matrix + a 1x3 matrix containing the translations.
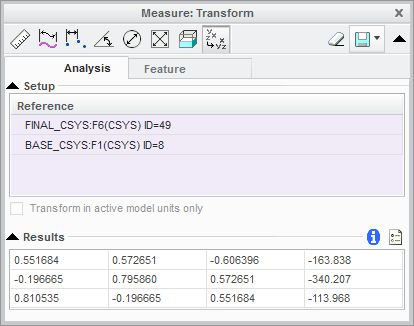
Problem here:
1) how do I get the 3 rotational parameters to use in the CSYS feature?
2) how do I get these 12 values in parameters to be able to use them in the first place? If I try to save this measurement as a feature, it throws me an error saying this type of measurement isn' t possible to save as a feature.
Conclusion: this doesn't work either.
Both ways work for static situations, but if I try to alter anything, the measurement is lost.
Any ideas?
- Tags:
- claw
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now I am understanding the use case. Thank you for explaining that.
I have never understood the transform matrix so that is not something I've ever worked with.
I am going to suggest you will need to interpolate the raw data from the 6 values provided by the CSYS feature itself. You will also need to keep track of the type of coordinate system the CSYS' are tied to in order to make the calculations.
I know this is a long string of calculations since you have to account for every CSYS in between.
It is not impossible, but there certainly is not a easy way to do it that I know of with only the data one can gather, save, and remain dynamic.
However, that is not to say you cannot do this with geometry. You can always place points, curves, planes, axes, sketches, etc between the primary and final CSYS features and act on them. They will remain dynamic and analysis data can be derived from them not to mention using the geometry to place yet another CSYS to always remain the same as the CSYS of interest. You just cannot get the data back reliably from what I can tell since you cannot save the matrix analysis feature.
I suspect there is an idea or two in this exercise. I suspect this basic knowledge to the mathcad guys.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You might see if this will read back what you need: (set to HD!)
This uses points to create a couple of curves to mimic the CSYS.
The beauty is that this is the values remain fully dynamic. Even with mechanism, the values update on the fly.
Creo 2.0 file attached.
- Tags:
- video
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is indeed a very interesting video.
It helped me understanding my issue.
I did some experiments, in combination with info about Euler, mentionned by David below.
But it seems that it's still not 100% what I'm looking for.
The formula's to calculate the Euler angles need other values in the rotation matix.
I'm currently investigating how to transform the matrix in this example to the correct one I can use to calculate the Euler angles.
Update:
It seems all components of the actual rotation matrix are the sinuses of the angles shown in the video example, except for the sign.
The angles in the measurement are always positive.
I think it's necessary to add a zero-reference or something like that to check if an angle is positive or negative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jeroen, I can't view the example file. It wants me to login. Can you upload it here? Use the advanced editor to upload it.
It's unfortunate that the transform can't be saved as a feature. Furthermore, it looks like Creo is calculating the matrix on the fly and not saving the information anywhere. Saving the analysis (saved analysis not feature) didn't have any benefit either. The only thing I could think of using the transform method would be to create a mapkey that creates or updates a csys based on the transform. When doing a transform measure or a summary measure you can view in the information window and then save the transform as a .trf file somewhere. Then you can create a csys or edit the definition of an existing csys and use the saved file. Creo then computes the corresponding angles and distances from the transform matrix in the file. This works but will not be automatic as you desire.
The portion of the matrix comprised of 3x3 values are basically cos, sin, etc. of the angle for the axis. You can calculate the angle by using atan2 and I can write out the formulas but it doesn't help in this situation since there is no way to directly grab the values for each location in the matrix. You could write a relation that would read them into variables and then compute the angles but that's more work with the same results of saving a transform file... a manually updated csys with a mapkey. I briefly looked at the program for the part and didn't see anything there either.
Your best bet is to use the method Antonius mentions above since the values are stored with the feature and writing a relation for each value to the new coordinate system can be done easily. I can't image why it wouldn't be working, I'd need to take a look at the example file to see how you have set up your part/assembly references.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A 4 X 3 matrix in this case is called an "augmented matrix," though it is usually handled as a 4 x 4.
The upper left 3 X 3 part of the matrix is responsible for the rotation, the top 3 entries of the 4th column are the translation, and the bottom row is all zeros. When multiplied by a [X Y Z 1] matrix, (note the added 4th column is the number one), the zeros in the 4 X 4 clean out the translation from the rotation, and then the 1 in the 1 X 4 matrix adds the translation back in.
Rather than doing something special, the augmented matrix lets any routine that can multiply two matrices handle the simultaneous multiplication and addition problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jeroen,
I'm having the same problem as you had: I have a CSYS and I would like to know the 3 distances and the 3 angles. So that I can reproduce the CSYS with these 6 parameters.
I've read this complete explanation a few times, and it looks all great. But I'm not a mathematician. So I don't know how to interpret the matrix and the Euler Angles and all stuff.
I've also downloaded your example files, but this doesn't make me any wiser either...
Can you tell me how which feature relations you created to read the 6 location parameters?
Jeroen Bruyndonckx wrote:
The way I first tried it, is based on Antonius' post: Create a new CSYS (1) on top of the one you would like to get the information from, and in the orientation tab, select "orient by selected CSYS axes". Here you select the reference CSYS.
Afterwards, create feature relations (2) for this new CSYS to read the 6 location parameters, and put them in feature parameters.
These parameters I can use to create a new CSYS (3) directly referenced to the base CSYS.
Thanks for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To simplify - you don't want to create a new coordinate system at the end of the mechanism chain, you want to know the cumulative transform from the start of the chain to the end of the chain.
I'd have a try by creating datum points at the (0,0,0), (1,0,0), (0,1,0), and (0,0,1) locations relative to the csys at the end of the chain. You should be able to get the values for each of the X, Y, and Z components in any other Csys.
Obviously, (0,0,0) -> translation. I haven't done it, but finding the Euler angles from the rest is a problem already solved. Search Google for "Calculation of Euler angles.pdf" It's on geom3d.com
One difficulty is the potential for gimbal-lock, which I think is dealt with in the above PDF as an exception.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a very interesting post!
I looked for these Euler formulas, and they should be able to do the trick!
I tried to make this work using the matrix that is generated by the piece of code that was posted by Antonius above. The Euler-calculation works like a charm, but the matrix from Antonius' post contains the data in another format.
At this moment I'm searching for a way to translate the matrix with angles to the correct rotation matrix needed to use in the Euler calculation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try these under the matrix composition section:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which leads you to the Creo rotation matrix format of:
X11 X12 X13 PX
X21 X22 X23 PY
X31 X32 X33 PZ
X11-X33 = rotation, PX-PZ = position. You will need to be careful about the angle ranges input into the equations. I don't know if this and the previous posts have information that was posted in David's link above since the website is blocked at work. If so, sorry for the duplicate information.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok,
problem 'solved'...
I used the information provided by Antonius, David and Eric, and I mixed them into a solution.
I now have a piece of code/features/measurements where I can make a UDF from to use in my components.
It's a bit more complex as imagined beforehand, but it works like a charm now.
If you are interested, I enclosed the part. All information to create a new CSYS is in the last feature (EULER_ANGLES)
Thank you all!
PS: I got in touch with someone from PTC, but they told me it wasn't possible in any way to get this information in an easy way, unless you should program it with pro/toolkit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Congratulations Jeroen! This is quite a feat. Thank you for putting all our knowledge together for a fine result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Measuring the center of mass also gives you also 3 angles, it seems to me that they are the Euler angles in the sequence yzx.
It could be easy to create a body constrained to a coordinate system.





