Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Community
- Creo+ and Creo Parametric
- Analysis
- Re: Dynamic frequency analysis from unconstrained ...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Dynamic frequency analysis from unconstrained modal analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dynamic frequency analysis from unconstrained modal analysis.
Dear Creo Simulate users (unfortunately a shrinking class)
I am trying to evaluate vibration induced stress in an assembly, but I do not have much background in this area, especially with Creo Simulate. Thus I am learning it with a simple model.
I am using as guideline the good presentation “Linear Dynamic System Analyses with Creo Simulate” by Roland Jakel. It contains a nice background but still not enough for my case.
I would like to simulate an unconstrained assembly and sweep a frequency. In this condition (unconstrained modal analysis) Creo Dynamic frequency analysis only accept load input.
As load input I chose to use acceleration. I can choose that the gravity stays constant for the entire frequency range (uniform) or it increases as the frequency increases, converting frequency and amplitude in acceleration using the function a = -(2*Pi*Freq)^2 * wave amplitude.
The procedure in Creo has some tricks but I think I could manage it. A simple CAD example is included.
I also took the chance and practiced how to mimic unconstrained structures using constrains – as for example using 3-2-1 point constrain or, for my simple plate example, constraining a point located at CG using a weak 6DOF spring.
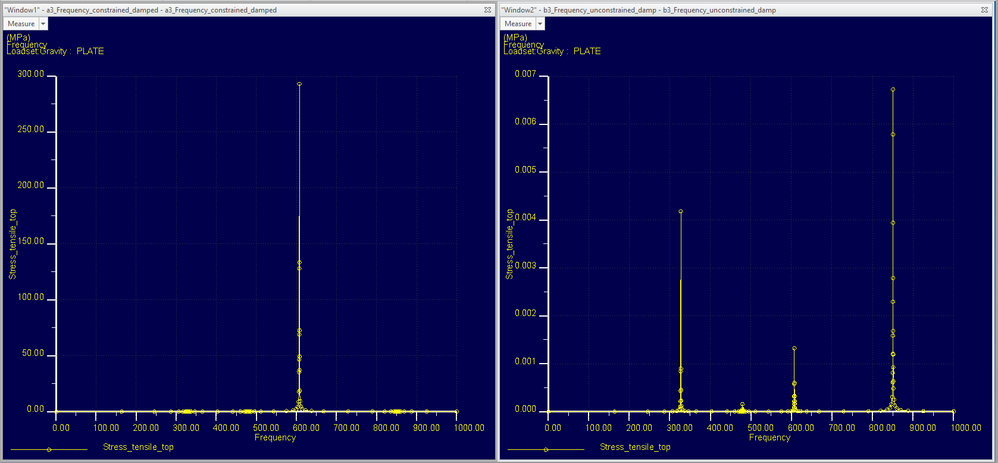
In the attached CAD model the constrained / unconstrained models have the same modal shape and eigenmodes. Nevertheless, the Dynamic frequency analysis shows very different values!
Why?!? Are the models incomparable even if they seems to show the same dynamic response? Can I really obtain reliable and physically meaningful measurements in an unconstrained structure?
Also introducing damping (even if very small – 0.01%) creates very different results among the same simulation (damping/no damping) or between constrained/unconstrained. I was surprised to see a so strong effect in the result.
And specifically for Creo Simulate, what is the meaning (and influence) of “Measure output steps per master step”? Should I use more than 1?
Also, Is it possible to import a “user defined master steps”? Here I would like to include each eigenmode found in the modal analysis for visual post-evaluation and it will be very boring doing this manually if dozen of eigenmodes are found in the modal analysis range.
Thank you very much for any feedback!
- Labels:
-
Simulate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are mixing up things here. Never heard of unconstrained sine sweep. The only thing I can think of is some sort of hammer test in a free-free mode to get modal data.
3-2-1 point constraint is not an unconstrained structure. Unconstrained means free-free i.e. NO constraint whatsoever
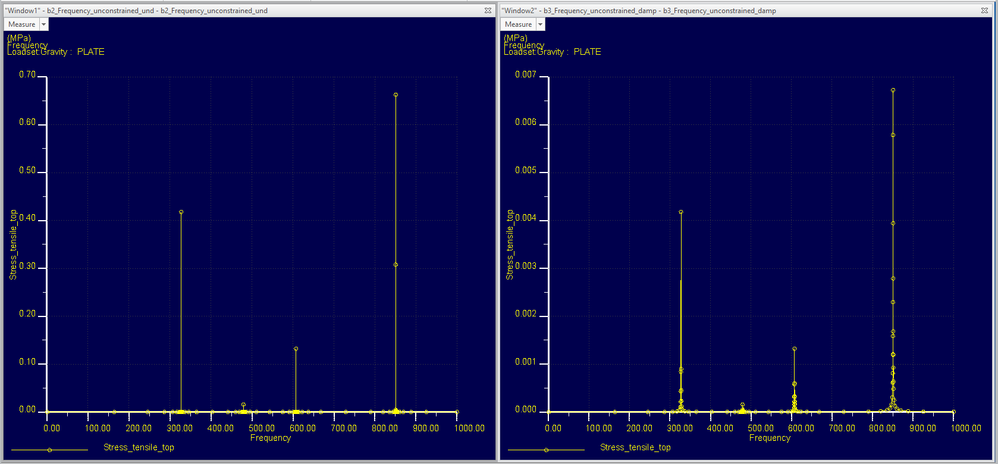
If you have, different constraints (constrained / unconstrained) models you will get different dynamic behaviours! You 1st set of windows is clearly showing this. Looking at the graphs your constrained model is clearly stiffer as only one mode exists in the range up to 1000Hz. The “unconstrained” model has four modes it seems in that range !
Obviously damping/no damping will create different (peak) response at the resonance. With no damping at resonance a SDoF response is infinite (in theory)
No idea what ‘Measure output steps per master step’ is but a wild guess it is referring to the (frequency) step you are using to define your input. 1Hz frequency step!
Looking at dozen of mode shape (eigenvector) might be very boring but it’s the nature of the job. Looking at your dummy bottom graphs one would only look at mode 1 & 4 (highest response). Mode 2 is clearly not responding in the direction you are exciting your structure. Have a look and understand the use of Modal Effective Mass
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks,
To apply a sin sweep in a constrain is the classical approach - for example is what a shaker would do.
I did not main to say that 3-2-1 is unconstrained - I said that it could be used to mimic the behavior of a free-free body since it will not overconstrain it. But even so, it may not match the modes. The location of a 3-2-1 constrain will change the modal shapes. This is easier to see in a plate.
For this reason I choose to constrain the CG of the plate with a very soft spring. The picture below shows the constrained and unconstrained shapes from 1 to 1000Hz. They have always the same shape.
Here the hint. Even being soft, the mode at 607Hz (mode 3) is located in the CG constrain. This amplify the bending movement in the rest of the plate instead of a translate it, as when unconstrained.
This explain why I see a peak in 607Hz for the constrained graph but not in the unconstrained one.
Also the "problem" with damping is explainable. As you pointed out it comes from "infinite" to something. Indeed a long way :-). Obviously, as my damping values gets smaller the results gets closer to the non-damping simulation. So yes, it is "very sensitive" if compared with a non-damping simulation.
Still, here comes back my problem.
How to perform in Creo a dynamic frequency analysis of an object that is "floating" but under a sinusoidal excitation between a frequency range from X to Y Hz?
_ A balloon/airplane with a shaker inside.
_ An object immersed in liquid receiving shock waves at different frequencies.
_ An object that is floating but under a magnetic field that changes polarity at different frequency.
_ Etc.
I do not need an detailed interaction with the environment (if so I would need a multi physics simulation). In reality these are not really "unconstrained" objects but very difficult to simulate its real constrain. And anyway, they tend to behave as free-free bodies!
_ Is my approach to use acceleration as input load and an unconstrained body correct to verify stresses in a specific frequency range? I do not visualize another way to setup this simulation in Creo.
Regarding ‘Measure output steps per master step’, it is there since "ever" but yet no clear documentation. Because it is old does not means that everyone know how to use it!
_ And to speed up the analysis at each normal mode, I think I could replace my amplitude function in the load set by a function definition that comes from a table. Now for each natural frequency I have a specific amplitude.
If this works, it also may need to check the box of "include frequency steps from table function" - because alone this is another command that I have no idea how to use because there is no way to include a table in the "user defined input steps" option.
Thank you again from your time!