Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
2D to 3D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2D to 3D
Hello folks,
does anybody know how to turn this oiecewise defined graph into a 3D plot?
Thanks in advance
Raiko
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery and Werner
thank you both for your response.
I just noticed that I had a typo in my message "oiecewise" instead of "piecewise". What I meant was the following:
To display one function is simple, but how do I define two consecutive functions that can be displayed in one 3D graph? f(x) and h(x) in my instance.
For that I do need advice
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have two functions of one variable: f(x) and h(x). For a three-dimensional plot you need to specify the dependence on a second variable. f(x,y) and h(x,y).
Otherwise they're planar functions on an unspecified value of y.
What am I missing? Something like this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
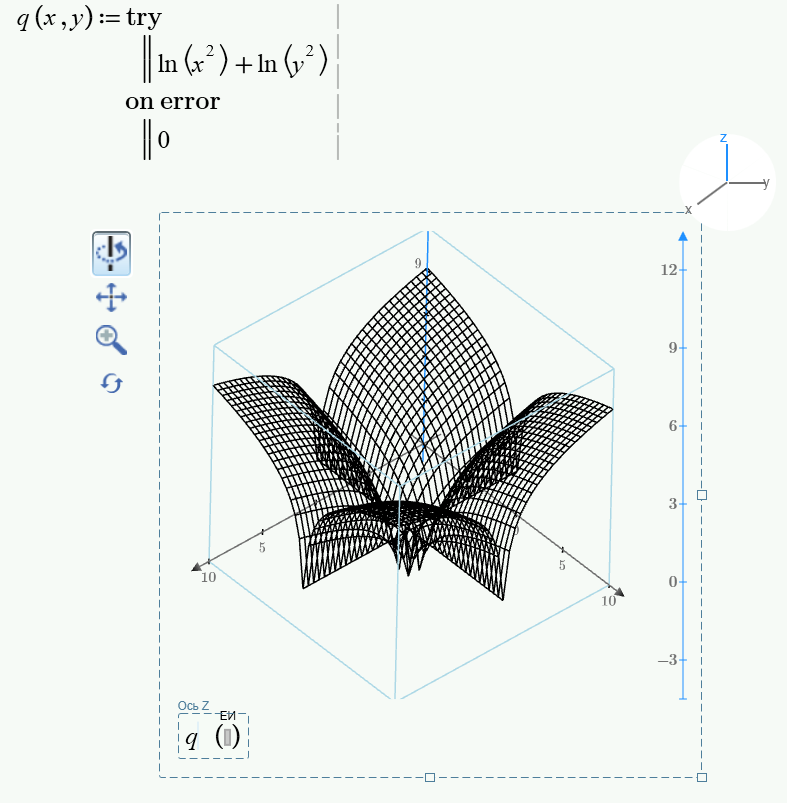
In Mathcad 15 you could use onerror similiar to what Valery had shown, but I would not return 0 in case of an error but rather a value like -10^(-8).
In Prime I would return NaN in case of error (unfortunately Mathcad 15 does not accept NaN in 3D plots).
You may also consider to simply chose a mesh which avoids zero values for x or y:
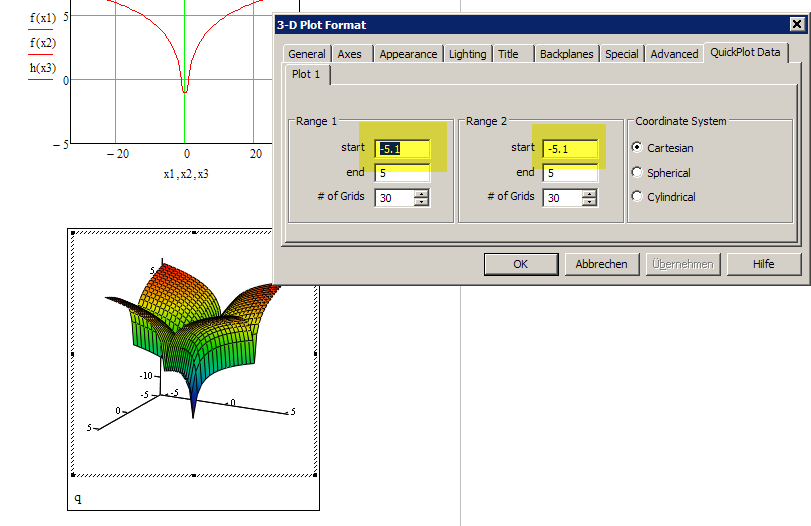
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> To display one function is simple, but how do I define two consecutive functions that can be displayed in one 3D graph? f(x) and h(x) in my instance.
??? Sorry, but I don't understand what you are looking for.
> does anybody know how to turn this oiecewise defined graph into a 3D plot?
How would you like to plot a function fx) in one independend variable (piecewise or not) into a 3D??
Fred had rotated your piciewise function around the z-axis.
I did something similar to what you tried with q(x,y)
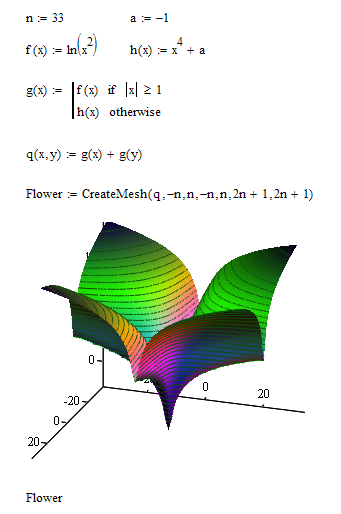
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, just now noticed that you tried to define a function M further down.
You defined local functions M instead of assigning the result a local variable M (you may chose any other name here).
Furthermore your condition was faulty. You cannot write "(x AND y)>1" but have to write "x>1 AND y>1". At least I guess that this is what you had in mind.
But your logic seems to be faulty - I guess you had something different in mind that what you get here.
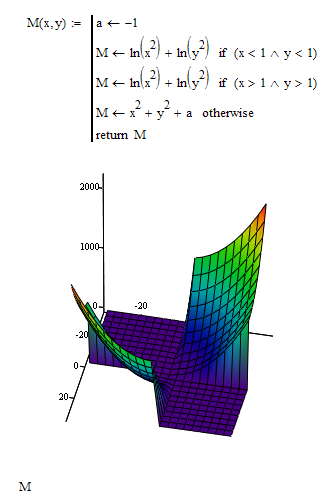
Just image where in the xy-plane the points are, where both x and y are either >1 or both are <1!

Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all for helping
Raiko





