Skip to main content
S
standish1-Visitor
1-Visitor
May 24, 2017
Question

2nd Order, Non-Linear ODE (Forced response/MCK system)

  • May 24, 2017
  • 6 replies
  • 5685 views

Dear All,

I am new to both MathCAD and the problem in hand, so have some novice questions and also hoping for some general strategy and where-to-go-from-here guidance …

I’ve derived an equation of motion for a mechanism, which is a 2nd order, non-linear ODE.  It’s an M-C-K type equation describing both angular and linear motion.  I’ve rewritten it with all angular terms re-defined as linear terms which has made it quite cumbersome.  I want to solve for displacement and time.

I tried using Odesolve, but couldn’t make this work with the full ODE (smaller chunks tested the syntax as OK, but seems it can’t cope with the full equation).  I’ve now manually re-written it as a 1st order equation and use rkfixed which seems to work.It's probably not the most elegant/efficient approach so will appreciate any suggestions for improvement here.

I stripped all units out while trying to make Odesolve work, and haven’t yet attempted to reinsert them, is doing so advisable with rkfixed?  I guess without units, the user must ensure the inputs are correct then apply units to the output manually?  I’ve currently used dummy values for constants while I worked on solving the ODE so the values won’t make sense yet.

Also, is it possible to use Lagrangian notation in rkfixed?  I found I had to swap to Leibniz to get it to work so the derivation (10 pages) uses one system and solution the other.  It would be nice to be consistent without having to re-write the whole derivation in Leibniz!

Having solved it with RKFixed, my challenge now is the equation contains a damping term which is a function of mechanism velocity.  This means I need to update that damping term (Moody friction factor) during the solution so damping corresponds to the calculated velocity - presumably this requires some programming in the solve process to update values? Could anyone point me at a good starting point for achieving this?  I hope I can just modify the existing content to interrupt the solve and execute a subroutine calculation at each time step, but haven’t started looking into it.  I’m up against a tight deadline so any pointers in that respect would also be appreciated!

Many thanks in anticipation,

Standish.

6 replies

F
Fred_Kohlhepp23-Emerald I
23-Emerald I
May 25, 2017

You're using version 15, so you must take out units in the ode solvers.

As useful function is "UnitsOf()"

There is also "State Space," which looks like it might be a way for you to go.

S
standish1-VisitorAuthor
1-Visitor
May 25, 2017

Thank you Fred.

I had a quick look at State Space, but think I'll need to implement it to understand it fully.  Will come back and let you know how I got on, having to do some reporting just now.

Best regards,

Standish.

M
mvenich14-Alexandrite
14-Alexandrite
May 25, 2017

> it can’t cope with the full equation

What's the full equation?

S
standish1-VisitorAuthor
1-Visitor
May 25, 2017

Thanks for your reply Martin,

Apologies.. the one in my attachment is the full equation.

I had tried smaller chunks of it in ODEsolve to check I wasn't making an error with syntax or similar and found I could get solutions up to a point, but when I substituted the full equation (the one in my attachment) ODESolve stopped working. 

Clicking through the different numerical methods available under ODEsolve (Adams Bashforth, RK adaptive RKfixed etc) gave me the impression it was understanding the syntax but those methods were just unable to get a solution.  Can't remember the specific errors I was getting, sorry, but one was "unable to get a converged solution" or words to that effect.

I gave up and changed to the method in my attachment as suspected I was wasting time trying to get ODEsolve to do something it wasn't capable of (possibly because the highest order term is non-linear?).

S
standish1-VisitorAuthor
1-Visitor
May 25, 2017

Martin,

You mean the full equation including the velocity-dependant damping term, in place of  Cd*dy/dt...

I haven't got that far yet, I've been trying to get a framework in place to make sure I am on the right track in terms of solution methods (I wasn't even sure MathCAD was an appropriate tool until yesterday - I've very little experience with it).

The velocity damping force will look something like:

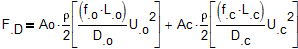
Where A = piston area, Roe = density, f = Moody friction factor, L = pipe length, D =pipe diameter, U = fluid velocity.

Subscripts o & c denote different regions of hydraulic control circuit.....

Once I've incorporated this in the equation I'll update.

-
-MFra-21-Topaz II
21-Topaz II
May 25, 2017

The equation is similar to this?

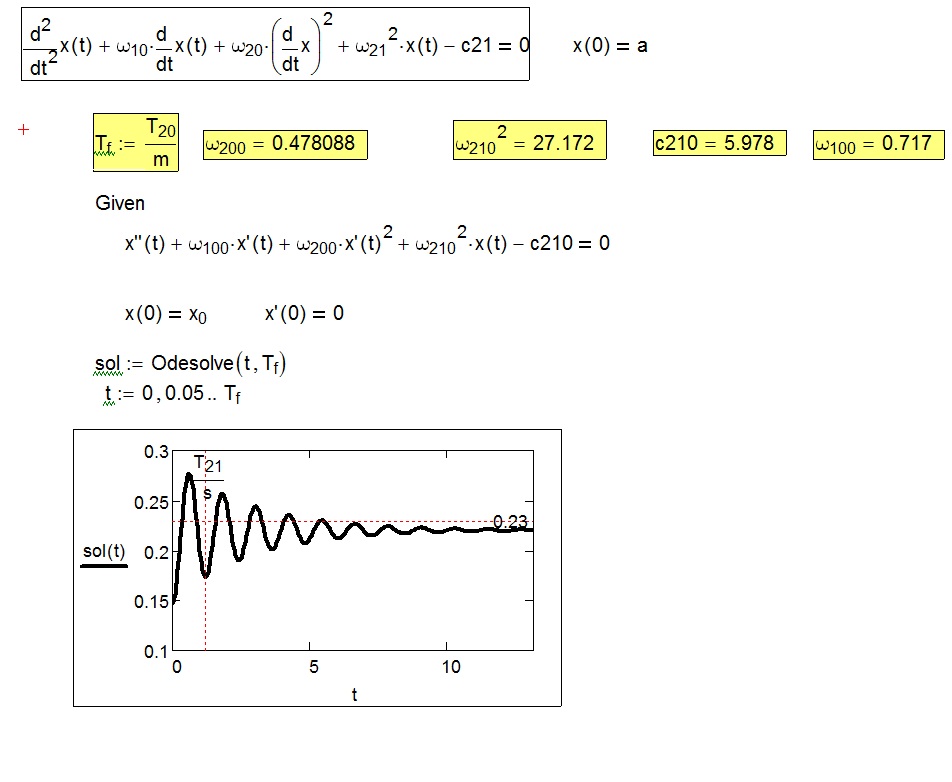
non linear equation.jpg

S
standish1-VisitorAuthor
1-Visitor
May 25, 2017

Hi F.M.

The full equation is the one in my attachment.  It is similar - both are 2nd order ODEs?

I have managed to get ODEsolve to solve other similar equations, just not the one in my attachment.  I suspect the ODEsolve is inappropriate, maybe due to non-linear highest order term, I'm not sure.

The RKFixed method shown in my attachment works anyway, so I'm now looking at how to adjust damping coefficients during solution, to reflect the calculated velocity.  Damping force and velocity are mutually dependent so I need to figure out how to build in that dependency and update damping at each timestep...

-
-MFra-21-Topaz II
21-Topaz II
May 25, 2017

Hi standish,

sorry, but when you put the question there was no attached file, so, without knowing your equation, I asked if it was similar to what I indicated. But I see that there are big differences.

F
Fred_Kohlhepp23-Emerald I
23-Emerald I
May 25, 2017

Attached is a forced response MCK solution with damping a function of velocity (a simple function, but a function.)

I hope it gives you a starting place.

-
-MFra-21-Topaz II
21-Topaz II
May 26, 2017

You have missed a simplification:

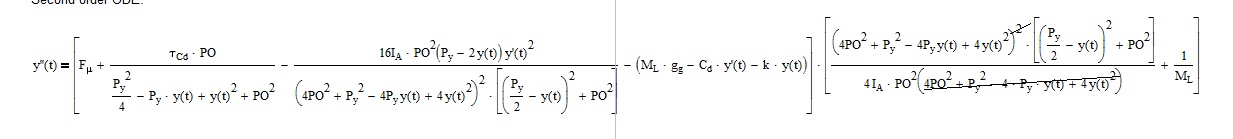
semplificazione.jpg

S
standish1-VisitorAuthor
1-Visitor
June 6, 2017

Hi F.M.,

Well spotted, thanks!

Just to update on this, I've been working on another problem since posting the inquiry but will update with the solution as soon as I've closed it out.

Kind regards,

Standish.

V
vlehner1-Visitor
1-Visitor
June 21, 2017

Hi Standish,

I got a solution with Odesolve - with negative t values and this is very strange.

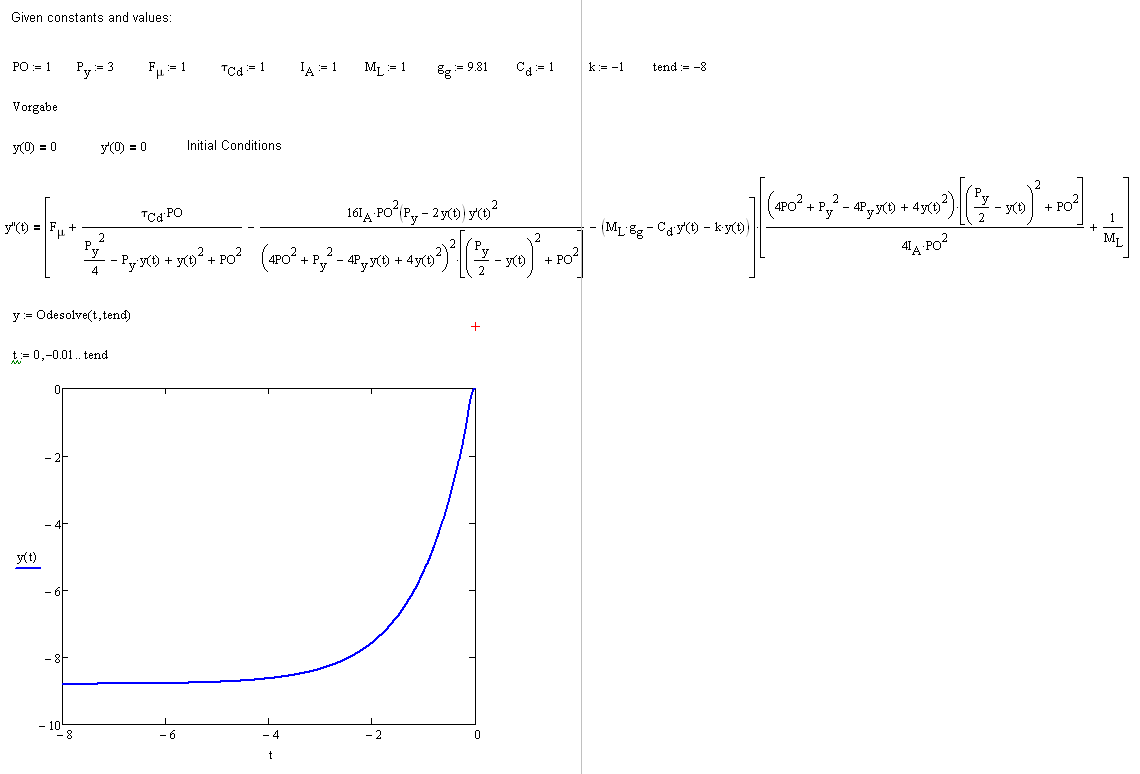
Can it be because of the equation?

What is the basically differential equation?

I need a physical description e.g a damped system with a spring etc.

Maybe i can give you the complete lagrangeschian formula of your system.

See Attachement please.

best regards, Volker

Terms & ConditionsCookie settingsAccessibility statement