Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
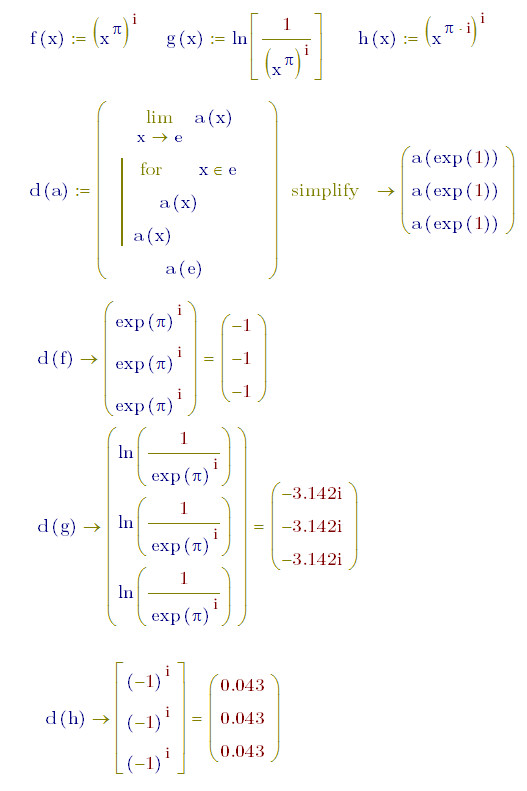
A Function and Three Output
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Function and Three Output
Hello Everyone,
I need help with explanation of each output.
Thanks in advance for your time and help.
Regards.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Loi Le wrote:
Hello Everyone,
I need help with explanation of each output.
Thanks in advance for your time and help.
Regards.
I'm guessing that you are querying why you have 3 different results?
As Werner says, the first result is correct ... as is the last result (it's just a substitution of x by e!) ... but I am intrigued by why the second result has been calculated in floating point.
You could look at the limits to see what the problem is at e ..
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should know that only the first result is correct and the other two are kind of "random numbers" due to bad round off errors. After all you try to divide by zero in a rather bizarre way.
Whats the point of this question? What are you trying to achieve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Loi Le wrote:
Hello Everyone,
I need help with explanation of each output.
Thanks in advance for your time and help.
Regards.
I'm guessing that you are querying why you have 3 different results?
As Werner says, the first result is correct ... as is the last result (it's just a substitution of x by e!) ... but I am intrigued by why the second result has been calculated in floating point.
You could look at the limits to see what the problem is at e ..
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
As Werner says, the first result is correct ... as is the last result (it's just a substitution of x by e!) ... but I am intrigued by why the second result has been calculated in floating point.
Yes, thats surprising. Guess it has something to do with the in(element of) operator/iterator.
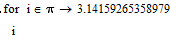
Here are some more surprising results:

The 23.14... are e^pi instead of e^(-pi).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I use "simplify", the problem seems be solved.
The "For" loop, I think the MuPad has looked it as a numerical calculation, and use a 10^-15 error on it; and the Maple has calculated it in symbolic totally.
Here is the Mathcad 15 result. I use e-10^-15 to correct the numerical error, and I get a good result.
The plot of the last function:

When the variable of the "For" loop output is a little large than e, even 10^-15, the function result is e^(pi).
And I have used the Mathcad 2001i to calculate the worksheet above without use the 10^-15 error correction, and have got a good result.