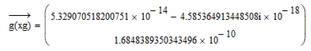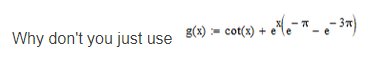Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A Reason for a missing-point ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Reason for a missing-point ?
Hello Everyone.
From :
Thanks in advance.
Regards.
Loi.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
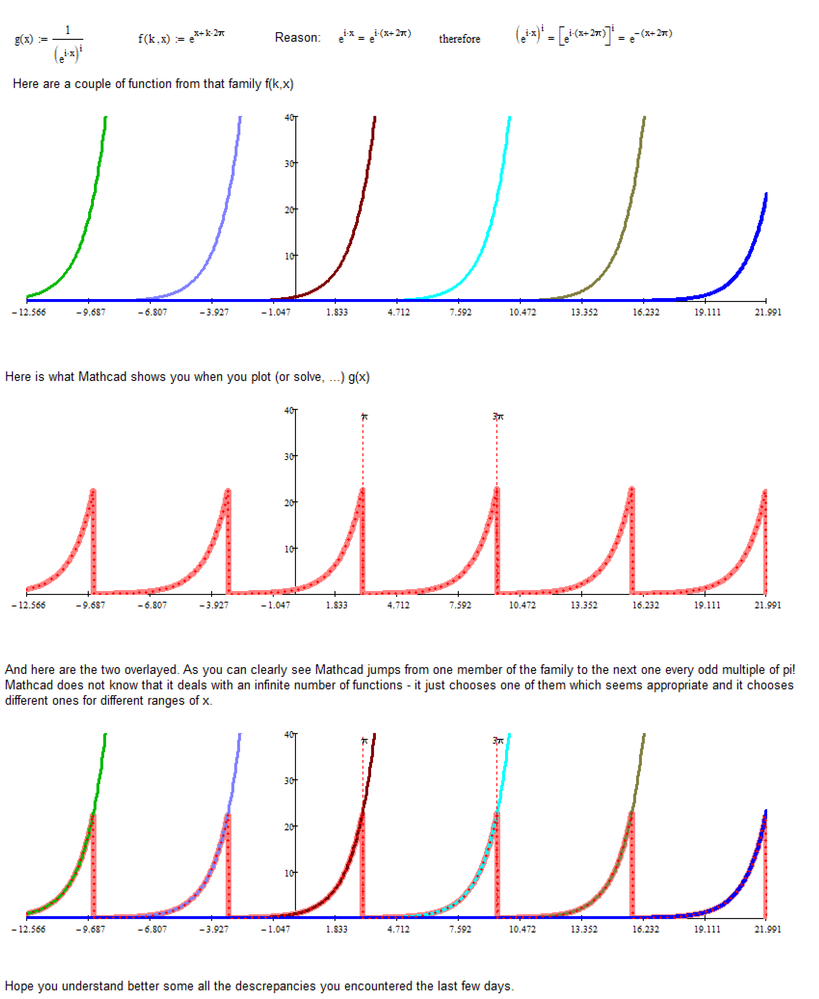
Again and again and again and again ....
You always run into numerical inaccuracies! You cannot expect a 100% exact result when using the numerics with its IEEE format and its limited about 15 digits precision.
The numerics in your case thinks that the first value is non-real and so it is not plotted:
In the meantime you should already know what to look for and be able to find out things like that yourself.
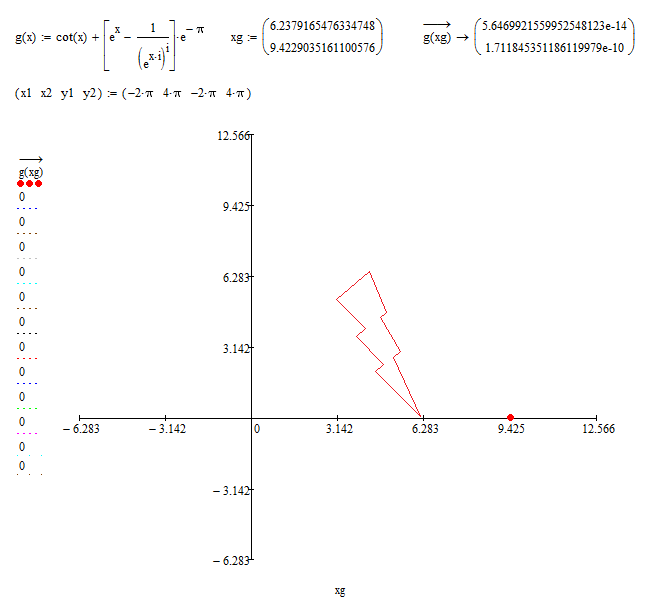
Why don't you just use
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess I don't fully understand above that, but a number with 30-decimal-digit It did show the point. And again : " I guess I don't fully understand above that " :

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh... so far I guess I somewhat understand about that, now the point to be shown but now I need help with a explanation.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you can see - the roots you have in mind are roots of DIFFERENT MEMBERS of that family.
Mathcad can't really deal with that kind of family of curves and "arbitrary" choses one, but not the same for every value of x you put in.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And again and again, so far the MATHCAD is the best one to me to use. And I have only a bit of knowledge and only about the MATHCAD. And I have not had any other Math software, but MATHCAD. And to me, the MATHCAD make MATH very simplest. As my demostration, The g(x) = cot(x) + e^(x)*{ e^-pi - e^(-3*pi) } and my function is NOT equivalent.
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now, anyway so far I still need help with a brief explanation about original question.
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You don't understand that "your" function is not just ONE single function but its an expression which splits into an infinite number of different functions.
You have no control over which of the many possible functions Mathcad uses when you let it calculate g(-2) or g(4) but chances are that Mathcad uses different ones.
Hope the following will make it clear to you, otherwise I can't help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For now , all words I have to say is I greatly appreciate your time and help.![]()
![]()
![]()
Best Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And : The g(k,x) = cot(x) + e^x*{ e^-pi - e^(2k-1)*pi } and g_(,x) = cot(x) + { {e^x - 1/{ [e^(x*1i)]^1i} }*e^-pi is NOT equivalent , EITHER :
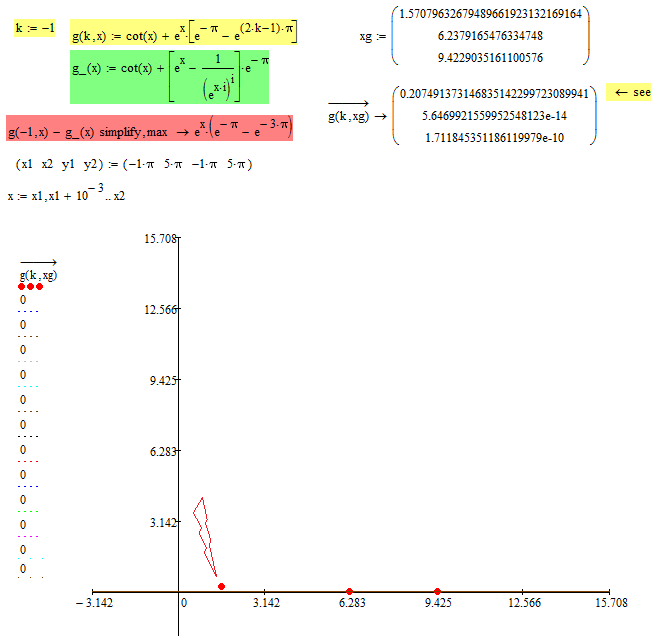
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now it's my turn to use :
and :
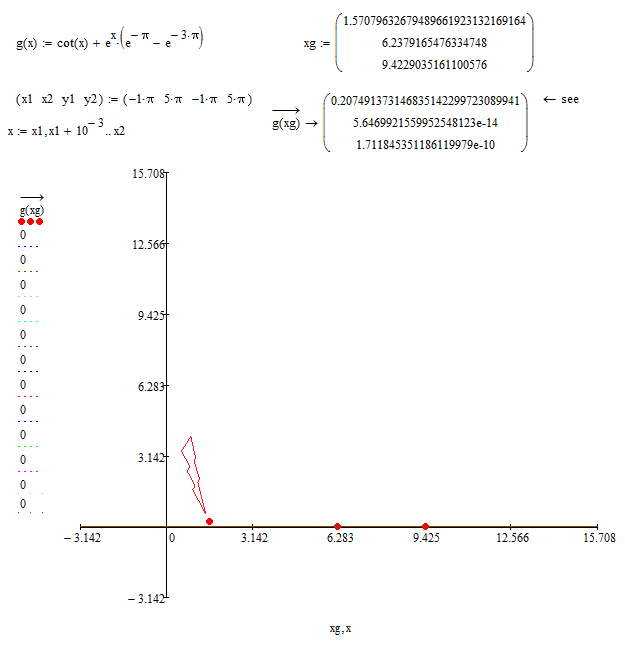
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and I guess : "The world is not the world".
Best Regards.
Loi.