Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A chain is thrown over two nails
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A chain is thrown over two nails
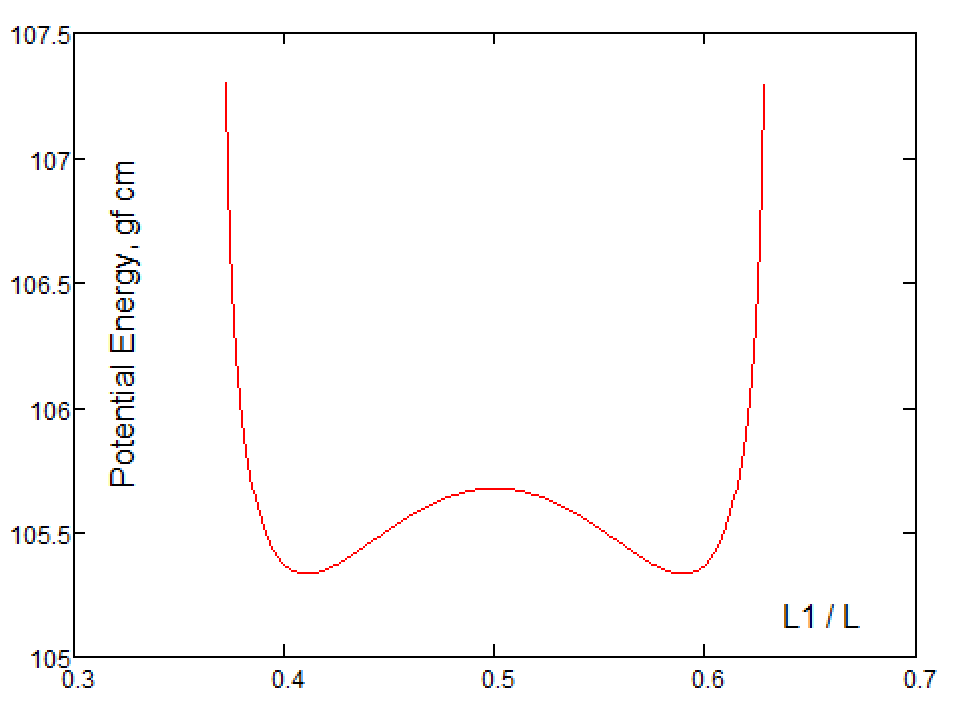
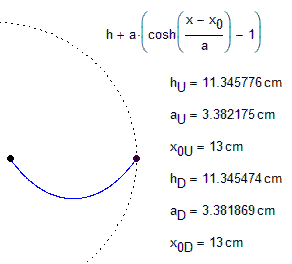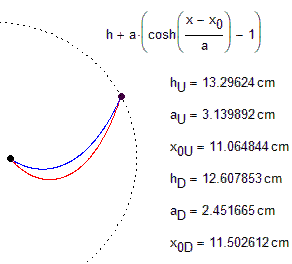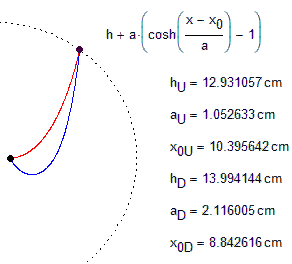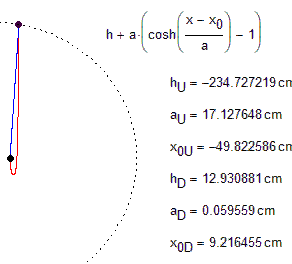
Inelastic flexible chain is thrown over two nails. There is no friction, no lock. How two parts of the chain are sagging. This system has one unstable equilibrium, when the length of the sagging sections of the chain are equal - see the Mathcad 15 sheet in attach. How to calculate two other stable equilibria, when one section of the chain approaches a straight line, but remains in the form of a catenary (see the picture).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One solution - an animation and a Mathcad 15 sheet in attach!
Do you know more interesting solution&
And second!
I have searched tis task in Internet - now results!
May be I have done something wrong!
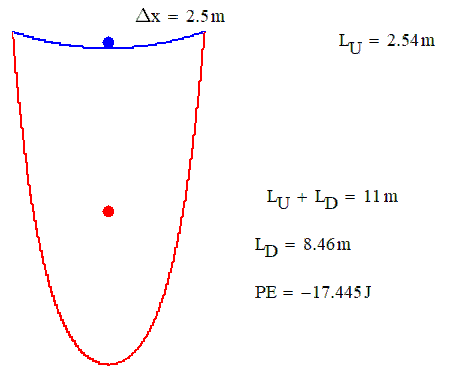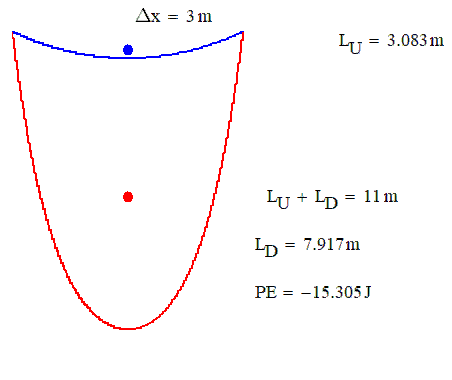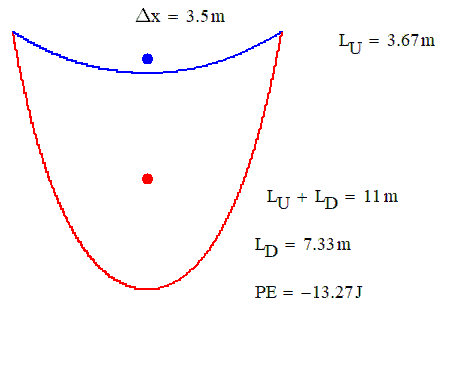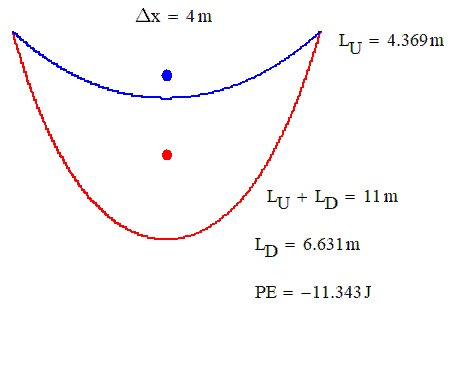
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
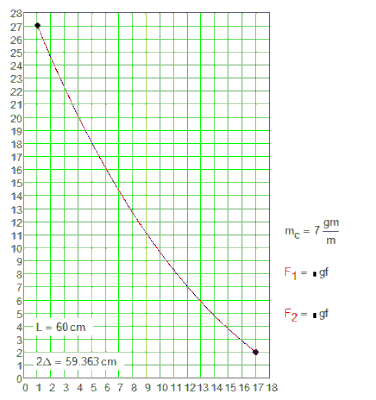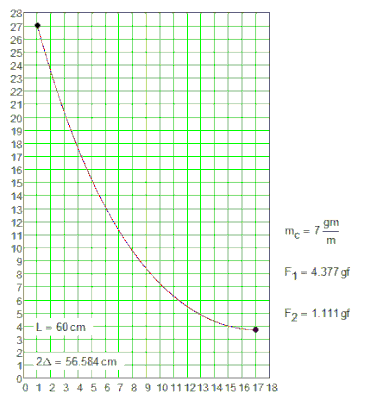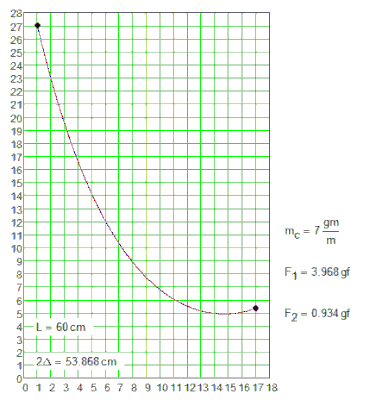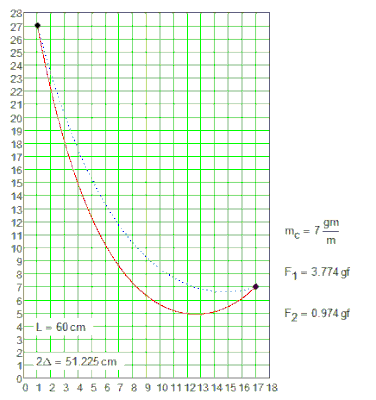
I see on the wall and calculate with Mathcad two cases:
1.
2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
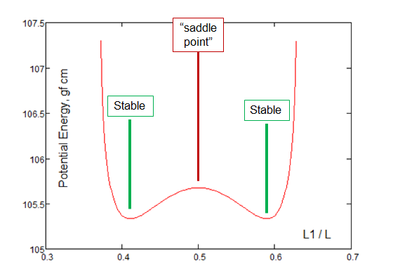
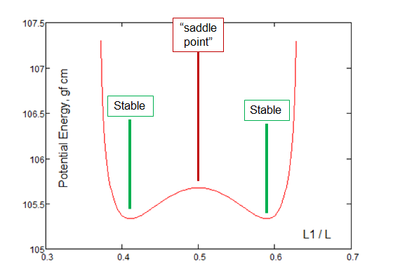
You second graph is the saddle point stability?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
You second graph is the saddle point stability?
I do not know!
I would like to understand this problem!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the two "loops" are equal length the system is stable; but if you make one just a bit longer (heavier) it will pull the other one until it's as long as it can be.
Loop A and Loop B
Saddle point stable: Loop A = Loop B
Stable 1: Loop A as long as possible, Loop B as short as possible
Stable 2: Loop B as long as possible, Loop A as short as possible
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very nice!
Anywhere the slope of your energy curve is zero is a "stable" point. But some are points to which the system will return while others are "saddle points." If a stable point is "perturbed" (move slightly off of the exact point) the system will return to the stable point. If a saddle point is perturbed, the system will move away from the saddle point. (The second derivative of energy tells the tale!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Very nice!
Anywhere the slope of your energy curve is zero is a "stable" point. But some are points to which the system will return while others are "saddle points." If a stable point is "perturbed" (move slightly off of the exact point) the system will return to the stable point. If a saddle point is perturbed, the system will move away from the saddle point. (The second derivative of energy tells the tale!)
There is not one but two case with the PE

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a sharp border between the case 1 and 2. Or it is a fuzzy border?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One boundary of numerical method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
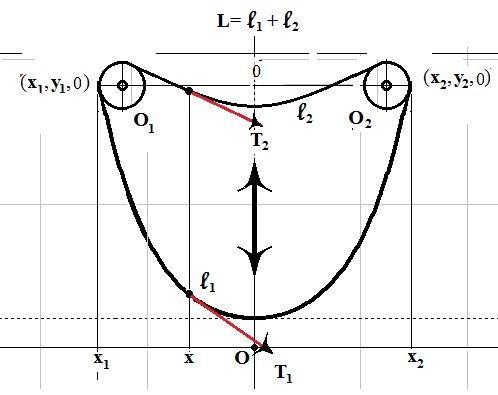
An animation closer to reality would be that of the following system .....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
An animation closer to reality would be that of the following system .....
No, closer to reality is that the tension in the two chains AT THE PULLEYS are equal, not at the same vertical points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
T1 and T2 are the tensions in the branches 1 and 2 at the same abscissa. In the drawing we can see that the two vectors T1 and T2 on the abscissa x, are different ....Even in the hypothesis in which the pulleys are of infinitesimal radius, the tensions on the pulleys are identical in magnitude if the only acting force is the gravitational one acting on the masses of the chains or belts..........
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like so?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
very beautiful. But the chain or the belt, it is too long .....furthermore it seems a transitory ... so there is friction .........