Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A question about a geometric series
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A question about a geometric series
Hi All, I am trying to solve a geometric problem.
A typical geometric series can be written like this, where N and M are two commensurable constants, i is the imaginary unit.
For this kind of geometric series, it can be derived by hand that it is equal to
If we are trying to solve this expression, by introducing a (k-1) as a coefficient of the exponential function, how can we solve it?
It is not necessarily to be done by Mathcad. Thank you!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simplify means just that. Its NOT an approximation, its an exact equivalent. So the answer to your question 1 is clearly YES.
Mathacds symbolics is sometimes quite tricky and its often hard to impossible to find out what keywords in what order to use to get the result in the way we expect it.
You see by my examples that the way Mathcad displays its result differs depending on how we tell Mathcad what to do.
I was surprised to see the much more compact result when I gave Mathcad the expression in q and then told it to substitute for the quotient of your example.
But Mathcad and especially its symbolic is always good for a surprise.
Symbolics is not the strongest part of Mathcad and so you may consider using Maple or Mathematica instead for more complicated symbolic calculations.
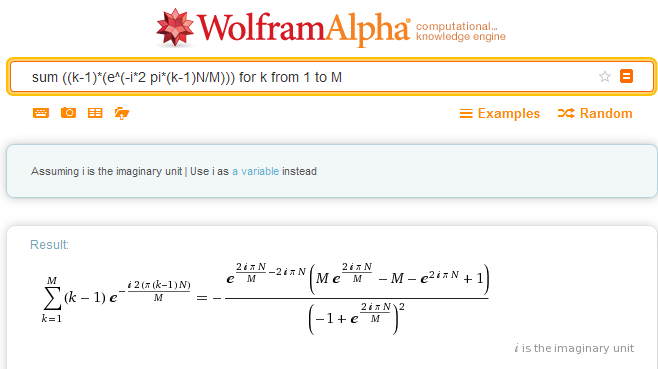
Also the free online Wolfram Alpha might be an option:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> If we are trying to solve this expression,
"solve" ???
I see no equations which could be solved (for which variable?).
I guess you know that your last expression is NOT a geometric series.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I did not mention it correctly. I want to know how to simplify this expression, by removing the Sigma symbol and write it as an expression whose manner is similar to
This is more like a mathematical question, but not Mathcad question.
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> This is more like a mathematical question, but not Mathcad question.
But you can use Mathcad to do the job 😉
Something like this:


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner Exinger, thank you so much for your advise. I have one question about the function of "simplify" here in your first pircture:
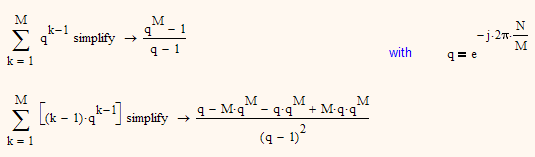
For the first simplify process, we know the result is the exact equivalent expression, not a "simplified" one.
My questions are :
(1) is the result in the second raw also the exact expression, instead of a "simplified" one?
(2) from the 2nd picture you posted, it seems like the answer of the question 1 is NO. Then would you tell me what kind of simplification Mathcad did?
(3) if the answer of the question 1 is YES, then that is what exactly I am looking for. Would you tell me the name of this kind of expression, then I can look for the references to derive the expression from the Left Hand Side of the "simplify" operation to the Right Hand Side?
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simplify means just that. Its NOT an approximation, its an exact equivalent. So the answer to your question 1 is clearly YES.
Mathacds symbolics is sometimes quite tricky and its often hard to impossible to find out what keywords in what order to use to get the result in the way we expect it.
You see by my examples that the way Mathcad displays its result differs depending on how we tell Mathcad what to do.
I was surprised to see the much more compact result when I gave Mathcad the expression in q and then told it to substitute for the quotient of your example.
But Mathcad and especially its symbolic is always good for a surprise.
Symbolics is not the strongest part of Mathcad and so you may consider using Maple or Mathematica instead for more complicated symbolic calculations.
Also the free online Wolfram Alpha might be an option:


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a different approach which displays the result in a different manner
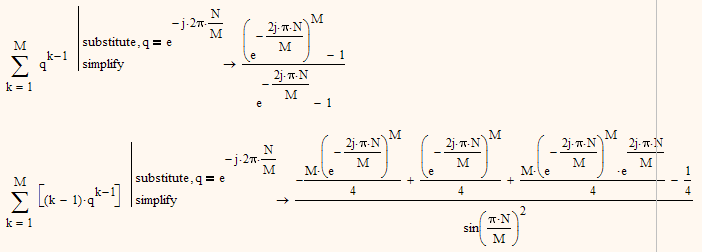
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Concerning the name of the series k*q^k.
I guess there is no special name. its just a variant of the geometric series.
You sure will find a lot of links where it is shown how to derive the closed formula for it
Power Sum -- from Wolfram MathWorld
https://de.wikipedia.org/wiki/Geometrische_Reihe#Herleitung_der_Varianten
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner Exinger, you helped me so much!





